Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

sinA/2.cos^3(B/2)=sinB/2.cos^3(A/2)
sinA/2.cos(B/2)[ 1 - sin^2B/2]=sinB/2.cos(A/2)[1 -sin^2A/2]
sinA/2.cosB/2 - sinB/2.cosA/2 = 1/2sinA/2.sinB/2[ sinB - sinA]
sin(A-B)/2 = sinA/2.sinB/2 cos(A+B)/2.sin(A-B)/2
sin(A-B)/2[ 1 - sinA/2.sinB/2 cos(A+B)/2] = 0
Vì [1 - sinA/2.sinB/2 cos(A+B)/2] >0
=> sin(A-B)/2 =0
=> A = B

Ta có : A+B+C= 180
=>sin(A+B)/2 = sin(180/2 - C/2) = cosC/2
ttcó: sinC/2 = cos(A+B)/2
=> sA+sB+sC =2cosC/2*cos(A-B)/2 + 2cos(A+B)/2*cosC/2
=2cosC/2
=4cosA/2cosB/2cosC/2

Bài 1:
a)
\(\sin ^2x+\sin ^2x\cot^2x=\sin ^2x(1+\cot^2x)=\sin ^2x(1+\frac{\cos ^2x}{\sin ^2x})\)
\(=\sin ^2x.\frac{\sin ^2x+\cos^2x}{\sin ^2x}=\sin ^2x+\cos^2x=1\)
b)
\((1-\tan ^2x)\cot^2x+1-\cot^2x\)
\(=\cot^2x(1-\tan^2x-1)+1=\cot^2x(-\tan ^2x)+1=-(\tan x\cot x)^2+1\)
\(=-1^2+1=0\)
c)
\(\sin ^2x\tan x+\cos^2x\cot x+2\sin x\cos x=\sin ^2x.\frac{\sin x}{\cos x}+\cos ^2x.\frac{\cos x}{\sin x}+2\sin x\cos x\)
\(=\frac{\sin ^3x}{\cos x}+\frac{\cos ^3x}{\sin x}+2\sin x\cos x=\frac{\sin ^4x+\cos ^4x+2\sin ^2x\cos ^2x}{\sin x\cos x}=\frac{(\sin ^2x+\cos ^2x)^2}{\sin x\cos x}=\frac{1}{\sin x\cos x}\)
\(=\frac{1}{\frac{\sin 2x}{2}}=\frac{2}{\sin 2x}\)
Bài 2:
Áp dụng BĐT Cauchy Schwarz ta có:
\(P=\frac{a^2}{\sqrt{a(2c+a+b)}}+\frac{b^2}{\sqrt{b(2a+b+c)}}+\frac{c^2}{\sqrt{c(2b+c+a)}}\)
\(\geq \frac{(a+b+c)^2}{\sqrt{a(2c+a+b)}+\sqrt{b(2a+b+c)}+\sqrt{c(2b+c+a)}}(*)\)
Tiếp tục áp dụng BĐT Cauchy-Schwarz:
\((\sqrt{a(2c+a+b)}+\sqrt{b(2a+b+c)}+\sqrt{c(2b+c+a)})^2\leq (a+b+c)(2c+a+b+2a+b+c+2b+c+a)\)
\(\Leftrightarrow (\sqrt{a(2c+a+b)}+\sqrt{b(2a+b+c)}+\sqrt{c(2b+c+a)})^2\leq 4(a+b+c)^2\)
\(\Rightarrow \sqrt{a(2c+a+b)}+\sqrt{b(2a+b+c)}+\sqrt{c(2b+c+a)}\leq 2(a+b+c)(**)\)
Từ \((*); (**)\Rightarrow P\geq \frac{(a+b+c)^2}{2(a+b+c)}=\frac{a+b+c}{2}=\frac{3}{2}\)
Vậy \(P_{\min}=\frac{3}{2}\)
Dấu "=" xảy ra khi $a=b=c=1$

Câu a)
Từ \(\tan a=3\Leftrightarrow \frac{\sin a}{\cos a}=3\Rightarrow \sin a=3\cos a\)
Do đó:
\(\frac{\sin a\cos a+\cos ^2a}{2\sin ^2a-\cos ^2a}=\frac{3\cos a\cos a+\cos ^2a}{2(3\cos a)^2-\cos ^2a}\)
\(=\frac{\cos ^2a(3+1)}{\cos ^2a(18-1)}=\frac{4}{17}\)
Câu b)
Có: \(\cot \left(\frac{\pi}{2}-x\right)=\tan x=\frac{\sin x}{\cos x}\)
\(\cos\left(\frac{\pi}{2}+x\right)=-\sin x\)
\(\Rightarrow \cot \left(\frac{\pi}{2}-x\right)\cos \left(\frac{\pi}{2}+x\right)=\frac{-\sin ^2x}{\cos x}\)
Và:
\(\frac{\sin (\pi-x)\cot x}{1-\sin ^2x}=\frac{\sin x\cot x}{\cos^2x}=\frac{\sin x.\frac{\cos x}{\sin x}}{\cos^2x}=\frac{1}{\cos x}\)
Do đó:
\(\Rightarrow \cot \left(\frac{\pi}{2}-x\right)\cos \left(\frac{\pi}{2}+x\right)+\frac{\sin (\pi-x)\cot x}{1-\sin ^2x}=\frac{1-\sin ^2x}{\cos x}=\frac{\cos ^2x}{\cos x}=\cos x\)
Ta có đpcm.

rút gọn biểu thức:
E=cos(\(\dfrac{3\pi}{3}-\alpha\))-sin(\(\dfrac{3\pi}{2}-\alpha\))+sin(\(\alpha+4\pi\))



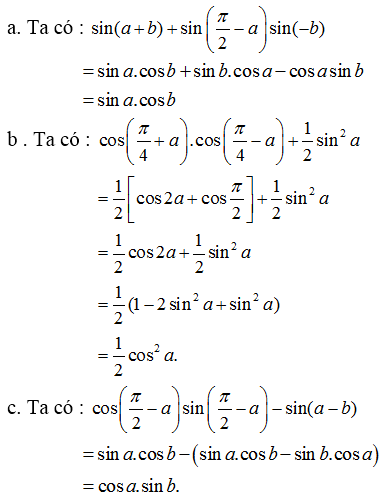
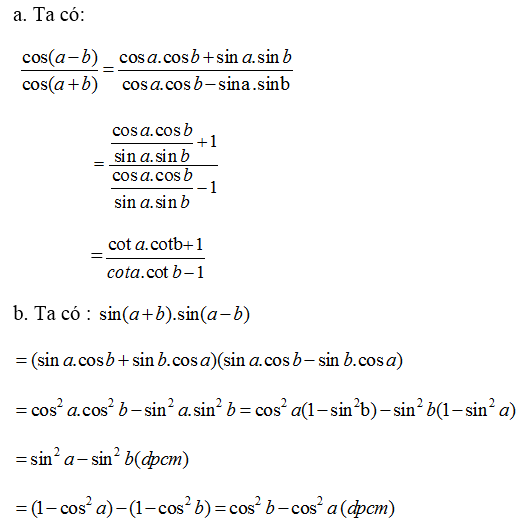
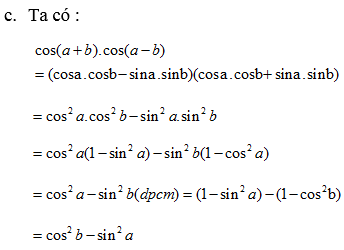
Lời giải:
\(\frac{1+\cos B}{\sin B}=\frac{2a+c}{\sqrt{(2a-c)(2a+c)}}\)
\(\Rightarrow \frac{(1+\cos B)^2}{\sin ^2B}=\frac{2a+c}{2a-c}\) (bình phương 2 vế)
\(\Leftrightarrow \frac{1+\cos ^2B+2\cos B}{\sin ^2B}=\frac{2a-c+2c}{2a-c}\)
\(\Leftrightarrow \frac{\sin ^2B+2\cos ^2B+2\cos B}{\sin ^2B}=1+\frac{2c}{2a-c}\)
\(\Leftrightarrow \frac{\cos ^2B+\cos B}{\sin ^2B}=\frac{c}{2a-c}\)
\(\Rightarrow (2a-c)(\cos ^2B+\cos B)=c\sin ^2B\)
\(\Leftrightarrow 2a\cos ^2B+(2a-c)\cos B=c\sin ^2B+c\cos ^2B=c(\sin ^2B+\cos ^2B)=c\)
\(\Leftrightarrow 2a(\cos ^2B+\cos B)=c(\cos B+1)\)
\(\Leftrightarrow (\cos B+1)(2a\cos B-c)=0\)
Với mọi \(\widehat{B}< 180^0\Rightarrow \cos B+1\neq 0\). Suy ra \(2a\cos B-c=0\Rightarrow \cos B=\frac{c}{2a}\)
Kẻ đường cao $CH$ xuống $AB$
\(\cos B=\frac{BH}{BC}=\frac{BH}{a}=\frac{c}{2a}\)
\(\Rightarrow BH=\frac{c}{2}\) hay $H$ là trung điểm của $AB$. Vậy $CH$ đồng thời là đường cao và đường trung tuyến, suy ra tam giác $ABC$ cân tại $C$