Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo bài ra ta có:
AB=8m => AO=OB=4m
AC=0,5m => OC=OA-AC=3,5m
=> Parabol đi qua điểm A(-4;0); B(4;0); C(-3,5; 2,93)
Do đó ta có các phương trình sau:
\(a.{( - 4)^2} + b( - 4) + c = 0 \Leftrightarrow 16a - 4b + c = 0\)
\(a{.4^2} + 4b + c = 0 \Leftrightarrow 16a + 4b + c = 0\)
\(a.{( - 3,5)^2} + b( - 3,5) + c = 2,93 \Leftrightarrow 12,25a - 3,5b + c = 2,93\)
Từ 3 phương trình trên, ta có: \(a = \frac{{ - 293}}{{375}};b = 0;c = \frac{{4688}}{{375}}\)
Tọa độ đỉnh là \(I\left( {0;\frac{{4688}}{{375}}} \right)\)
Vậy chiều cao của cổng parabol là \(\frac{{4688}}{{375}} \approx 12,5m\)
=> Kết quả của An tính ra không chính xác.

Gắn hệ trục Oxy vào chiếc cổng, gọi chiều cao của cổng là h ta vẽ lại parabol như dưới đây:
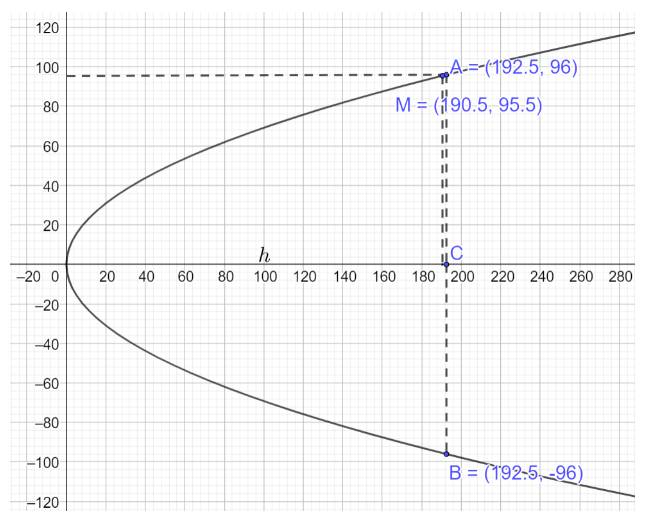
Phương trình parabol mô phỏng cổng có dạng \({y^2} = 2px\)
Theo giả thiết \(AB = 2{y_A} = 192 \Rightarrow {y_A} = 96,OC = h \Rightarrow M\left( {h - 2;95,5} \right),A\left( {h;96} \right)\)
Thay tọa độ các điểm \(M\left( {h - 2;95,5} \right),A\left( {h;96} \right)\) vào phương trình \({y^2} = 2px\) ta có:
\(\left\{ \begin{array}{l}95,{5^2} = 2p\left( {h - 2} \right)\\{96^2} = 2ph\end{array} \right. \Rightarrow \left\{ \begin{array}{l}p = \frac{{383}}{{16}}\\h \simeq 192,5\end{array} \right.\)
Vậy chiều cao của cổng gần bằng 192,5 m