Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x (đồng) là giá tiền một quả quýt và y (đồng) là giá tiền một quả cam. Điều kiện
x > 0, y > 0 ta có hệ phương trình:
\(10x+7y=17800\)
\(12x+6y=18000\)
<=> Hệ phương trình \(10x+7y=17800\)
\(2x+y=3000\)
<=> Hệ phương trình 2x + y = 3000
2y = 28000
<=> x= 800 và y = 1400.
Trả lời: Giá tiền một quả quýt: 800 đồng, một quả cam 1400 đông
Vân:10 quả quýt,7 quả cam=17 800 đồng
Lan:12 quả quýt,6 quả cam=18 000 đồng
Nếu cả số quýt và cam của vân mua gấp lên 2 lần thì đc
20 quýt+14 cam=35 600 đồng
-12 quýt+6 cam=18 000đông
=8 quýt+8 cam=17 600 đồng
giá tiền 1 quả quýt là: 17 600 -8=17 592 đồng
giá tiền1 quả cam là: 17 6 00- 17 592 =8

Gọi x và y lần lượt là giá tiền mỗi quả quýt và mỗi quả cam. (x > 0; y > 0)
Vân mua 10 quả quýt, 7 quả cam hết 17800 đồng nên ta có:
10x + 7y = 17800
Lan mua 12 quả quýt, 6 quả cam hết 18000 đồng nên ta có:
12x + 6y = 18000
Từ đó ta có hệ:
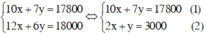
Từ (2) rút ra được y = 3000 – 2x, thay vào (1) ta được :
10x + 7.(3000 – 2x) = 17800
⇔ 10x + 21000 – 14x = 17800
⇔ 4x = 3200 ⇔ x = 800 (thỏa mãn)
Thay x = 800 vào y = 3000 – 2x ta được y = 1400 (thỏa mãn)
Vậy giá tiền một quả quýt là 800đ và giá tiền một quả cam là 1400đ.

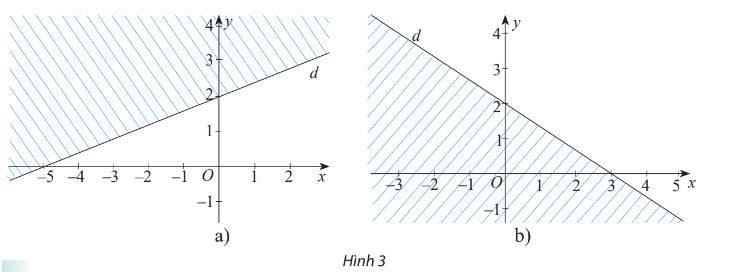
Gọi phương trình đường thẳng \(d:ax + by + c = 0\)
a) Từ hình a) ta thấy d đi qua hai điểm\(A(0;2)\) và \(B( - 5;0)\)
\( \Rightarrow \left\{ \begin{array}{l}b.2 + c = 0\\ - 5a + c = 0\end{array} \right. \Rightarrow c = 5a = - 2b\)
Chọn \(a = 2 \Rightarrow b = - 5;c = 10\) và \(d:2x - 5y + 10 = 0\)
Điểm O (0;0) thuộc miền nghiệm và \(2.0 - 5.0 + 10 = 10 > 0\)
Vậy bất phương trình cần tìm là \(2x - 5y + 10 > 0\)
b) Từ hình b) ta thấy d đi qua hai điểm\(A(0;2)\) và \(B(3;0)\)
\( \Rightarrow \left\{ \begin{array}{l}2b + c = 0\\3a + c = 0\end{array} \right. \Rightarrow - c = 3a = 2b\)
Chọn \(a = 2 \Rightarrow b = 3;c = - 6\) và \(d:2x + 3y - 6 = 0\)
Điểm O (0;0) không thuộc miền nghiệm và \(2.0 + 3.0 - 6 = - 6 < 0\)
Vậy bất phương trình cần tìm là \(2x + 3y - 6 > 0\)

Tham khảo:
Để pha x lít nước cam loại I cần 30x g bột cam,
Để pha y lít nước cam loại II cần 20y g bột cam,
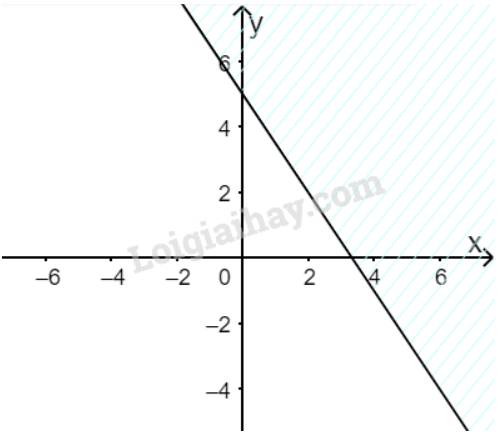
Vì Cúc chỉ có thể dùng không quá 100 gam bột cam nên ta có bất phương trình \(30x + 20y \le 100\)
\( \Leftrightarrow 3x + 2y - 10 \le 0\)
Vẽ đường thẳng \(\Delta :3x + 2y - 10 = 0\) đi qua hai điểm \(A(0;5)\) và \(B\left( {2;2} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(3.0 + 2.0 - 10 = - 10 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)

Để cam nhiều hơn thì sẽ có 3 th:
TH1: 2 cam, 1 mận, 1 xoài
=>Có \(C^2_8\cdot5\cdot4=560\)
TH2: 3 cam, 1 xoài
=>Có \(C^3_8\cdot4=224\left(cách\right)\)
TH3: 3 cam, 1 mận
=>Có \(C^3_8\cdot5=280\left(cách\right)\)
=>n(A)=280+224+560=1064
\(n\left(\Omega\right)=C^4_{17}=2380\)
=>P(A)=1064/2380=38/85

Gọi x là diện tích trồng đậu, y là diện tích trồng cà, (đơn vị a = 100 m 2 ), điều kiện x ≥ 0, y ≥ 0, ta có x + y ≤ 0
Số công cần dùng là 20x + 30y ≤ 180 hay 20 + 3y ≤ 18
Số tiền thu được là
F = 3000000x + 4000000y (đồng)
Hay F = 3x + 4y (đồng)
Ta cần tìm x, y thỏa mãn hệ bất phương trình
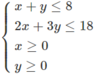
Sao cho F = 3x + 4y đạt giá trị lớn nhất.
Biểu diễn tập nghiệm của (H) ta được miền tứ giác OABC với A(0;6), B(6;2), C(8;0) và O(0;0).
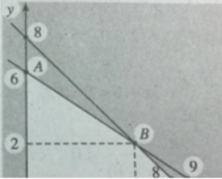
Xét giá trị của F tại các đỉnh O, A, B, C và so sánh ta suy ra x = 6, y = 2 (tọa độ điểm B) là diện tích cần trồng mỗi loại để thu được nhiều tiền nhất là F = 26 (triệu đồng).
Đáp số: Trồng 6a đậu, 2a cà, thu hoạch 26 000 000 đồng.

Giải:
2/3 cây cam = 3/5 cây quýt và = 6/7 cây vải thều hay 6/9 cây cam = 6/10 cây quýt = 6/7 cây vải thều
Vậy số cây cam chiếm 9 phần, số cây quýt chiếm 10 phần và số cây vải thều chiếm 7 phần.
Số cây cam là: 1950 : ( 9 + 10 + 7 ) * 9 = 675 ( cây )
Số cây quýt là: 1950 : (9 + 10 + 7 ) * 10= 750 (cây)
Số cây vải thều là: 1950 - ( 675 + 750 ) = 525 (cây)
Đ/S: Cam : 675 cây ; quýt : 750 cây ; vải thều : 525 cây .
![]()