Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: p + e = n = 82
Mà p = e, nên: 2p + n = 82 (1)
Theo đề, ta có: 2p - n = 22 (2)
Từ (1) và (2), ta có HPT:
\(\left\{{}\begin{matrix}2p+n=82\\2p-n=22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2n=60\\2p-n=22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=30\\p=26\end{matrix}\right.\)
Vậy p = e = Z = 26 hạt, n = 30 hạt.
Dựa vào bẳng hóa trị, suy ra:
X là sắt (Fe)
Theo đề, ta có:
\(\left\{{}\begin{matrix}2\cdot Z+N=82\\2\cdot Z-N=22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}Z=26\\N=30\end{matrix}\right.\)
hay A=56
\(X=^{26}_{56}FE\)

Z = số proton = số electron. N = số nơtron
Theo đề bài ta có : 2Z + N = 34
Ta biết rằng trong hạt nhân, số nơtron bao giờ cũng bằng hoặc lớn hơn số proton (trừ trường hợp duy nhất là hiđro có Z = 1).
N > Z. Vì vậy ta có : 3Z < 34, do đó Z < 34/3 = 11,3 (1)
Cũng vì N ≥ Z nên theo điều kiện của đề bài Z < 20, do đó :
N/Z ≤ 1,2 → N ≤ 1,2Z
Từ đó ta có : 2Z + N < 2Z + 1,2Z
34 < 3,2 => Z > 34/3,2 = 10,6 (2)
Tổ hợp (1) và (2) ta có : 10,6 < Z < 11,3 mà Z nguyên. Vậy Z = 11. Đó là nguyên tố natri có 11 proton, 11 electron, 12 nơtron.
Số khối của nguyên tử : A = Z + N = 23 => NTK là 23

M chiếm 52,94% về khối lượng:
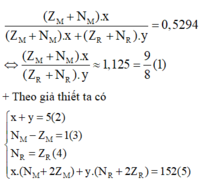
Quan sát – phân tích: Để tìm câu trả lời cho bài toán ta chỉ cần xác định được 4 ẩn x;y; Z M ; Z R
Vì vậy ta sẽ tìm cách khử các ẩn không cần thiết bằng cách thế phương trình (3) và (4) lầ lượt vào phương trình (1) và (5):
Thế (3) và (4) vào phương trình (1) ta được:
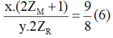
Thế (3) và (4) vào phương trình (5) ta được:
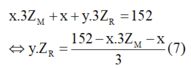
Quan sát – phân tích: Ba phương trình (2); (6); (7) với 4 ẩn ta nghĩ ngay đến biện luận để tìm nghiệm.
Thế (7) vào (6) ta được
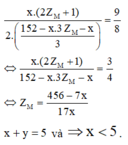
Mặt khác x nguyên
x nhận các giá trị 1, 2, 3, 4
Ta có bảng sau:

=> Cặp nghiệm thỏa mãn: x = 2 và Z M = 13 ⇒ M là Al
Thay x và ZM vào (7) và (2) ta tìm được y =3 và Z R = 8 ⇒ R là Oxi
Do đó hợp chất X là Al2O3 tổng số proton trong X là 13.2 + 8.3 = 50
Đáp án B.

Ta có: \(\left\{{}\begin{matrix}p+e+n=82\\p=e\\n-p=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3p=78\\p=e\\n=p+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}p=e=26\\n=30\end{matrix}\right.\)
\(\Rightarrow A=p+n=26+30=56\left(u\right)\)

Ta có: \(1\le\dfrac{N}{Z}\le1,5\)
\(\Rightarrow Z\le N\le1,5Z\)
\(\Rightarrow3Z\le2Z+N\le3,5Z\)
Vậy ta có : \(3Z\le24\le3,5Z\)
=> \(6,86\le Z\le8\)
=>\(\left[{}\begin{matrix}Z=7\left(N\right)\\Z=8\left(O\right)\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}N=10\\N=8\end{matrix}\right.\)
Mà theo đề bài : \(1\le\dfrac{N}{Z}\le1,5\)
=> Chỉ có O thỏa mãn
=> Z là O , số P= số E =8 , N=8
b) Cấu hình E: 1s22s22p4

Đáp án A
Theo giả thiết ta có:
2 Z X + N X = 23 8 Z Y ( 1 ) 2 Z Y + N Y = 16 5 Z X ( 2 ) N X + N Y = 2 Z Y ( 3 )
⇒ - 6 5 Z X + - 7 8 Z Y + N X + N Y = 0 ( 1 ) + ( 2 ) N X + N Y = 2 Z Y ( 3 )
⇔ 9 8 Z X = 6 5 Z X ⇔ Z X Z Y = 15 16

\(A=2Z+N\\ Z=\dfrac{A-N}{2}\)