Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khối lượng riêng của nguyên tử là:
D = 19,36.100/74 = 26,16(g/ cm 3 )
Khối lượng của 1 mol nguyên tử :
M = V.D.N = 4/3π r 3 .D.N = 4/3. 3,14. 1 , 44 . 10 - 8 3 .26,16. 6,022. 10 23 ≈ 197 (g/mol)

Theo bài ra thể tích của 1 mol Au là \(\frac{197}{19,36}\left(g/cm^3\right)\)
Đặt x % là thể tích các nguyên tử Au trong tinh thể, thì thể tích thực của một nguyên tử Au:
\(V=\frac{197}{19,36}\times\frac{x}{100\times6,02\times10^{23}}\)
Mặt khác với bán kính nguyên tử Au là 1,44 x 10−8 cm ta có:
\(V=\frac{4}{3}\times3,14\times\left(1,44\times10^{-8}\right)^3cm^3\)
⇒ x = 73,95%
Tham khảo nha !

hể tích của 1 phân tử Fe
V(Fe) = 4π/3. r˄3 = 4π/3 . (1,28.10˄-8)˄3 = 8,78.10˄-24 cm˄3
Thể tích của 1 mol Fe:
V = V(Fe).Na/74% = 8,78.10˄-24.6,022.10˄23/0,74 = 7,15cm˄3
Khối lượng riêng của Fe:
d = 56/7,15 = 7,83g/cm˄3

Đề bài tóm tắt:
- Nguyên tử Fe có:
- Bán kính nguyên tử: \(r = 1 , 28 \textrm{ } \overset{\circ}{\text{A}} = 1 , 28 \times 10^{- 10} \textrm{ } \text{m}\)
- Khối lượng mol nguyên tử: \(M = 56 \textrm{ } \text{g}/\text{mol} = 0 , 056 \textrm{ } \text{kg}/\text{mol}\)
- Trong tinh thể: nguyên tử chiếm 74% thể tích.
- Tính khối lượng riêng của Fe trong tinh thể.
Bước 1: Khối lượng của 1 nguyên tử Fe
Số Avogadro: \(N_{A} = 6 , 022 \times 10^{23}\) nguyên tử/mol
\(m_{\text{Fe}} = \frac{M}{N_{A}} = \frac{0 , 056}{6 , 022 \times 10^{23}}\) \(m_{\text{Fe}} \approx 9 , 30 \times 10^{- 26} \textrm{ } \text{kg}\)
Bước 2: Thể tích hình cầu nguyên tử Fe
\(V_{\text{c} \overset{ˋ}{\hat{\text{a}}} \text{u}} = \frac{4}{3} \pi r^{3} = \frac{4}{3} \pi \left(\right. 1 , 28 \times 10^{- 10} \left.\right)^{3}\) \(V_{\text{c} \overset{ˋ}{\hat{\text{a}}} \text{u}} \approx 8 , 78 \times 10^{- 30} \textrm{ } \text{m}^{3}\)
Bước 3: Thể tích thực tế trong mạng tinh thể
Do các nguyên tử chỉ chiếm 74% thể tích:
\(V_{\text{th}ự\text{c}\&\text{nbsp};\text{t} \overset{ˊ}{\hat{\text{e}}}} = \frac{V_{\text{c} \overset{ˋ}{\hat{\text{a}}} \text{u}}}{0 , 74}\) \(V_{\text{th}ự\text{c}\&\text{nbsp};\text{t} \overset{ˊ}{\hat{\text{e}}}} \approx \frac{8 , 78 \times 10^{- 30}}{0 , 74} \approx 1 , 19 \times 10^{- 29} \textrm{ } \text{m}^{3}\)
Bước 4: Khối lượng riêng
\(\rho = \frac{m_{\text{Fe}}}{V_{\text{th}ự\text{c}\&\text{nbsp};\text{t} \overset{ˊ}{\hat{\text{e}}}}} = \frac{9 , 30 \times 10^{- 26}}{1 , 19 \times 10^{- 29}}\) \(\rho \approx 7 , 8 \times 10^{3} \textrm{ } \text{kg}/\text{m}^{3}\)
✅ Kết quả:
\(\boxed{\rho \approx 7 , 8 \textrm{ } \text{g}/\text{cm}^{3} = 7 , 8 \times 10^{3} \textrm{ } \text{kg}/\text{m}^{3}}\)
cho tui 1 tick nha


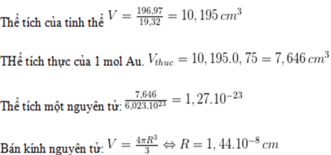
 bài giải đây nha!
bài giải đây nha!
Theo bài ra thể tích của 1 mol Au là \(\dfrac{197}{19,36}\) (g/cm3).
Đặt x % là thể tích các nguyên tử Au trong tinh thể, thì thể tích thực của một nguyên tử Au:
V=\(\dfrac{197}{19,36}\)×\(\dfrac{x}{100.6,02.10^{23}}\)
Mặt khác với bán kính nguyên tử Au là 1,44 x 10−8 cm ta có:
V=\(\dfrac{4}{3}.3,14.\left(1,44.10^{-8}\right)^3\left(cm^3\right)\)
⇒ x = 73,95%