Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Gọi số khối của X lần lượt là A1, A2, A3
Ta có hệ
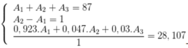
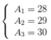

Gọi số khối của X là A1, A2, A3:
Ta có hệ:\(\left\{{}\begin{matrix}\text{A1+A2+A3=87}\\\text{A2-A1=1}\\\frac{0,923.A_1+0,047.A_2+0,03+A_3}{1}=28,107\end{matrix}\right.\)➝\(\left\{{}\begin{matrix}A_1=28\\A_2=29\\A_3=30\end{matrix}\right.\)
Đáp án C

Đáp án C
Gọi số khối của ba đồng vị tương ứng x1, x2, x3
Ta có x2= x1 +1
Theo đề ra ta có hệ phương trình
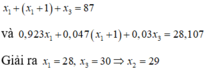

Tổng số khối 3 đồng vị X1,X2,X3 là 87 nên ta có pt:
\(A_{X1}+A_{X2}+A_{X3}=87\left(1\right)\)
Vì X2 có nhiều hơn X1 là 1 hạt notron, nên ta có pt:
\(N_{X2}-N_{X1}=1\\ \Leftrightarrow A_{X2}-A_{X1}=1\left(2\right)\)
Mặt khác, khối lượng nguyên tử trung bình là 28,0855 đ.v.C nên ta có pt:
\(\dfrac{A_{X1}.92,23\%+A_{X2}.4,67\%+A_{X3}.3,1\%}{100\%}=28,0855\left(đ.v.C\right)\left(3\right)\)
Từ (1), (2), (3) ta lập được hệ 3pt và giải tìm nghiệm được:
\(\left\{{}\begin{matrix}A_{X1}\approx28\left(đ.v.C\right)\\A_{X2}\approx29\left(đ.v.C\right)\\A_{X3}\approx30\left(đ.v.C\right)\end{matrix}\right.\)
\(b.\left\{{}\begin{matrix}P_{X1}+N_{X1}=28\\P_{X1}=N_{X1}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}P_{X1}=14\\N_{X1}=14\end{matrix}\right.\\ \Rightarrow N_{X2}=29-14=15\left(hạt\right)\\ N_{X3}=30-14=16\left(hạt\right)\)

A1+A2+A3=87
- Khối lượng của 1 nguyên tử X=5621,4/200=28,107
- Ta có: 92,3A1+4,7A2+3A3=28,107.100=2810,7
- Ngoài ra: A2-A1=1
Giải hệ 3 phương trình trên ta có được:
A1=28
A2=29
A3=30
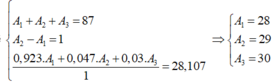
A1+A2+A3=87(1)
A2-A1=1(2)
\(\dfrac{92,3A_1+4,7A_2+3A_3}{100}=28,107\)
92,3A1+4,7A2+3A3=2810,7(3)
Giải hệ phương trình 1,2,3 ta được:
A1=28, A2=29 , A3=30
- Trong A1: A1=P1+N1=28 , do P1=N1 nên P1=N1=14
- Trong A2:
N2=N1+1=14+1=15\(\rightarrow\)P2=A2-N2=29-15=14
- Trong A3=30:
P3=14\(\rightarrow\)N3=16