Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
+ Mức cường độ âm tại điểm M là trung điểm của AB được xác định bởi:
L M = 10 log P I 0 4 π S M 2 ↔ log P 10 - 12 4 π . 70 2 → P = 6 , 2 . 10 - 4 W.
→ Năng lượng giới hạn bởi hai mặt cầu E = P t = P A B v = 6 , 2 . 10 - 4 100 340 = 1 , 81 . 10 - 4 J.

Đáp án C
Công thức chung cho điểm M cách nguồn O 1 đoạn MO: I M = P 4 π M O 2 = I 0 .10 L M
Áp dụng công thức với:
+ Điểm A: khi có 1 nguồn âm: P 4 π A O 2 = I 0 .10 3
+ Điểm B: khi có 1 nguồn âm: P 4 π B O 2 = I 0 .10 L B
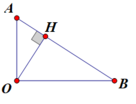
+ Điểm H: (chân đường vuông góc kẻ từ O đến AB) đây là điểm có mức cường độ âm lớn nhất vì gần nguồn nhất. Có 64 P 4 π H O 2 = I 0 .10 5
Có tam giác OAB vuông tại O, OH vuông góc AB
=> 1 O H 2 = 1 O A 2 + 1 O B 2 ⇒ 10 3 + 10 L B = 10 5 64 ⇒ L B = 2 , 75 ( B )

Đáp án B
+ Gọi O là vị trí đặt nguồn âm. Ta có:
L A - L B = 20 log OB OA ⇒ OB = 10 OA
Để đơn giản cho tính toán, ta chuẩn hóa OA = 1.
+ Từ hình vẽ, ta có
OM = OA 2 + AM 2 = 1 2 + ( 10 - 1 ) 2 ≈ 2 , 38 .
→ Mức cường độ âm tại M: L M = L A + 20 log ( 2 , 38 ) ≈ 32 , 46 dB .
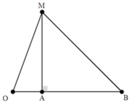

- Ta có hình vẽ:
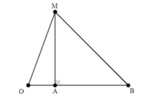
- Gọi O là vị trí đặt nguồn âm. Ta có:
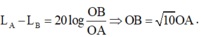
- Để đơn giản cho tính toán, ta chuẩn hóa OA = 1.
- Từ hình vẽ, ta có:
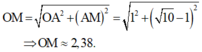
- Suy ra: mức cường độ âm tại M:
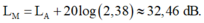


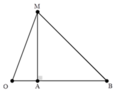

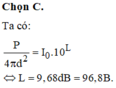
S A B C
Áp dụng CT: \(L_A-L_B=20.\lg\dfrac{SB}{SA}\)
Suy ra: \(50-30=20.\lg\dfrac{SB}{SA}\)
\(\Rightarrow \dfrac{SB}{SA}=10\)
Tương tự: \(L_A-L_C=20.\lg\dfrac{SC}{SA}=20.\lg\dfrac{SA+SB}{2.SA}=20.\lg(5,5)\)
\(\Rightarrow L_C=50-20\lg(5,5)=35dB\)
Mà: \(L_C=10\lg\dfrac{I_C}{I_0}\)
\(\Rightarrow I_C=10^{-12}.10^{3,5}=3,15.10^{-9}(W/m^2)\)