Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Diện tích bề mặt của mỗi tầng (kể từ tầng 1) lập thành một cấp số nhân có công bội ![]()
Khi đó diện tích mặt trên cùng là: ![]()
Chọn A.

THeo đề bài, đường kính của hình tròn đáy của nón bằng 2a. Vậy bán kính R = a.
Chiều cao của hình nón bằng chiều cao của tam giác đều, nên h = a√3 và
đường sinh l = = 2a.
Vậy diện tích xung quanh của hình nón là:
Sxq = πRl = 2a2π ( đơn vị diện tích).
Thể tích khối nón là:
.
Câu hỏi nào của Võ Nguyễn Thái cũng có Võ Đoong Anh Tuấn làm,có khúc mắc

\(\left(C_1\right)\) có dạng \(y=x^3-3x\)
Gọi điểm A(a;2) là điểm kẻ đc 3 tiếp tuyến đến C do đề bài yêu cầu tìm điểm thuộc đường thẳng y=2
ta tính \(y'=3x^2-3\)
gọi \(B\left(x_0;y_0\right)\) là tọa độ tiếp điểm
phương trình tiếp tuyến tại điểm B có dạng
\(y=y'\left(x_0\right)\left(x-x_0\right)+y_0\)
suy ra ta có \(y=\left(3x^2_0-3\right)\left(x-x_0\right)+x_0^3-3x_0\)
do tiếp tuyến đi qua điểm A suy ra tọa độ của A thỏa mãn pt tiếp tuyến ta có
\(2=\left(3x^2_0-3\right)\left(a-x_0\right)+x_0^3-3x_0\Leftrightarrow-\left(3x^2_0-3\right)\left(a-x_0\right)+x_0^3-3x_0-2=0\Leftrightarrow-3\left(x_0-1\right)\left(1+x_0\right)\left(a-x_0\right)+\left(1+x_0\right)^2\left(x_0-2\right)=0\)(*)
từ pt * suy ra đc 1 nghiệm \(x_0+1=0\Rightarrow x_0=-1\) hoặc\(-3\left(x_0-1\right)\left(a-x_0\right)+\left(1+x_0\right)\left(x_0-2\right)=0\)(**)
để qua A kẻ đc 3 tiếp tuyến thì pt (*) có 3 nghiệm phân biệt
suy ra pt (**) có 2 nghiệm phân biệt khác -1
từ đó ta suy ra đc a để pt có 2 nghiệm phân biệt khác -1
suy ra đc tập hợ điểm A để thỏa mãn đk bài ra

Đáp án C
Xét trường hợp A P P C = k , lúc này M P // B C nên B C // M N P .
Ta có: N ∈ M N P ∩ B C D B C // M N P B C ⊂ B C D ⇒ B C D ∩ M N P = N Q // B C , Q ∈ B D .
Thiết diện là tứ giác MPNQ.
Xét trường hợp A P P C ≠ k .
Trong A B C gọi R = B C ∩ M P .
Trong B C D gọi Q = N R ∩ B D thì thiết diện là tứ giác MNPQ.
Gọi K = M N ∩ P Q . Ta có S M N P S M N P Q = P K P Q .
Do A M N B = C N N D nên theo định lí Thales đảo thì A C , N M , B D lần lượt thuộc ba mặt phẳng song song với nhau và đường thẳng PQ cắt ba mặt phẳng này tương ứng tại P, K, Q nên áp dụng định lí Thales ta được P K K Q = A M M B = C N N D = k
⇒ P K P Q = P K P K + K Q = P K K Q P K K Q + 1 = k k + 1

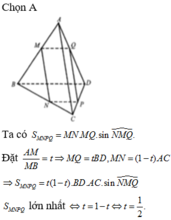
Đáp án là B