Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tần số lớn nhất là 31
=>Nhóm chứa mốt là [60;80)
j=4
a4=60
m4=31; m3=23; m5=29; h=20
Do đó, ta có:
\(M_0=60+\dfrac{31-23}{\left(31-23\right)+\left(31-29\right)}\cdot20=76\)
=>Đa số các con ong có tuổi thọ là 76 ngày

Tham khảo:
Mẫu a, b là mẫu số liệu ghép nhóm.
a)

- Có 5 sinh viên chi dưới 50 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 12 sinh viên chi từ 50 đến dưới 100 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 23 sinh viên chi từ 100 đến dưới 150 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 17 sinh viên chi từ 150 đến dưới 200 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 3 sinh viên chi từ 200 đến dưới 250 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
Như vậy, đa số sinh viên chi từ 100 đến dưới 150 nghìn đồng mỗi tháng cho cước điện thoại và có ít sinh viên chi trên 200 nghìn đồng cho cước điện thoại mỗi tháng.
b)

- Có 7 ngày có nhiệt độ từ đến dưới.
- Có 15 ngày có nhiệt độ từ đến dưới.
- Có 12 ngày có nhiệt độ từ đến dưới.
- Có 6 ngày có nhiệt độ từ đến dưới.

Mẫu số liệu được chia thành 7 nhóm:
- Có 6 nhân viên có thời gian đi từ nhà đến nới làm việc là từ 15 đến dưới 20 phút.
- Có 14 nhân viên có thời gian đi từ nhà đến nới làm việc là từ 20 đến dưới 25 phút.
- Có 25 nhân viên có thời gian đi từ nhà đến nới làm việc là từ 25 đến dưới 30 phút.
- Có 37 nhân viên có thời gian đi từ nhà đến nới làm việc là từ 30 đến dưới 35 phút.
- Có 21 nhân viên có thời gian đi từ nhà đến nới làm việc là từ 35 đến dưới 40 phút.
- Có 13 nhân viên có thời gian đi từ nhà đến nới làm việc là từ 40 đến dưới 45 phút.
- Có 9 nhân viên có thời gian đi từ nhà đến nới làm việc là từ 45 đến dưới 50 phút.

a) Tổng số giá trị của mẫu số liệu là: 344 752 \( \times \) 4 = 1 379 008 giá trị.
b) Nếu lập bảng tần số cho mẫu số liệu (T) sẽ dễ hình dung được bức tranh tổng thể về kết quả thi vì giúp thuận lợi cho việc tổ chức đọc và phân tích số liệu.
c) Số lượng thí sinh có ít nhất một môn học có điểm dưới 6 là 23.
Số lượng thí sinh có ít nhất 1 môn học có điểm từ 6 đến dưới 7 là 69.
…
Số lượng thí sinh có tổng điểm 3 môn học từ 28 đến dưới 29 là 216.
Số lượng thí sinh có tổng điểm 3 môn học từ 29 đến 30 là 12.

a)
x | \( - \pi \) | \( - \frac{{2\pi }}{3}\) | \[ - \frac{\pi }{2}\] | \( - \frac{\pi }{3}\) | 0 | \(\frac{\pi }{3}\) | \(\frac{\pi }{2}\) | \(\frac{{2\pi }}{3}\) | \(\pi \) |
\(y = \cos x\) | -1 | \( - \frac{1}{2}\) | 0 | \(\frac{1}{2}\) | 1 | \(\frac{1}{2}\) | 0 | \( - \frac{1}{2}\) | -1
|
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;\cos x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) và nối lại ta được đồ thị hàm số \(y = \cos x\) trên đoạn \(x \in \left[ { - \pi ;\pi } \right]\) (Hình 27)
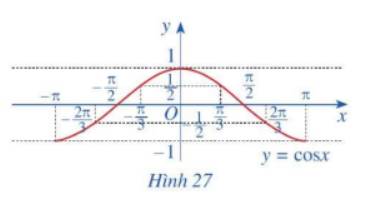
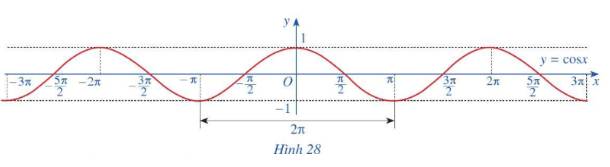
c) Làm tương tự như trên đối với các đoạn \(\left[ { - 3\pi ; - \pi } \right]\), \(\left[ {\pi ;3\pi } \right]\),...ta có đồ thị hàm số \(y = \cos x\)trên R được biểu diễn ở Hình 28.

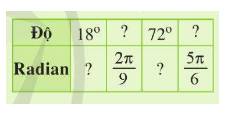
Ta có bảng chuyển đổi số đo độ và số đo radian của một số góc sau:
Độ | \({18^ \circ }\) | \(\frac{{2\pi }}{9}.\frac{{180}}{\pi } = {40^ \circ }\) | \({72^ \circ }\) | \(\frac{{5\pi }}{6}.\frac{{180}}{\pi } = {150^ \circ }\) |
Radian | \(18.\frac{\pi }{{180}} = \frac{\pi }{{10}}\) | \(\frac{{2\pi }}{9}\) | \(72.\frac{\pi }{{180}} = \frac{{2\pi }}{5}\) | \(\frac{{5\pi }}{6}\) |

Trong Hình 4b, góc lượng giác là (Oz,Ot) với tia đầu là tia Oz và tia cuối là tia Ot

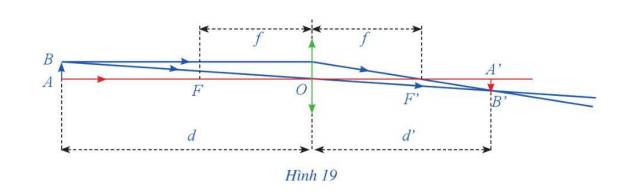
a) Ta có \(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f} \Leftrightarrow \frac{1}{{d'}} = \frac{1}{f} - \frac{1}{d} = \frac{{d - f}}{{df}} \Leftrightarrow d' = \frac{{df}}{{d - f}}\)
b)
Ta có: \(\left\{ \begin{array}{l}df > 0\\d - f > 0,d \to {f^ + }\end{array} \right.\)
\(\begin{array}{l}\mathop {\lim }\limits_{d \to {f^ + }} \varphi (d) = \mathop {\lim }\limits_{d \to {f^ + }} \frac{{df}}{{d - f}} = + \infty \end{array}\)
Ta có: \(\left\{ \begin{array}{l}df > 0\\d - f < 0,d \to {f^ - }\end{array} \right.\)
Do đó, \(\begin{array}{l}\mathop {\lim }\limits_{d \to {f^ - }} \varphi (d) = \mathop {\lim }\limits_{d \to {f^ - }} \frac{{df}}{{d - f}} = - \infty \end{array}\)
Vì \(\begin{array}{l}\mathop {\lim }\limits_{d \to {f^ + }} \varphi (d)\ne \mathop {\lim }\limits_{d \to {f^ - }} \varphi (d)\end{array}\)
Vậy nên không tồn tại \(\begin{array}{l}\mathop {\lim }\limits_{d \to f} \varphi (d) \end{array}\)
Giải thích ý nghĩa của các kết quả tìm được: Khi khoảng cách của vật tới thấu kính mà gần với tiêu cự thì khoảng cách ảnh của vật đến thấu kính ra xa vô tận nên lúc đó bằng mắt thường mình không nhìn thấy.

a)

Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng lớn (dần tới \( + \infty \)).
b)

Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng bé (dần tới \( - \infty \)).









Tần số lớn nhất là 31 nên nhóm chứa mốt là \(\left[ {60;80} \right).\;\)Ta có:
\(j = 4;\;\;{a_4} = 60;\;\;{m_4} = 31;\;\;{m_3} = 23;\;\;{m_5} = 29;\;\;h = 20\). Do đó,
\({M_0} = 60 + \frac{{31 - 23}}{{\left( {31 - 23} \right) + \left( {31 - 29} \right)}} \times 20 = 76\).
Ý nghĩa: Đa số các con ong có tuổi thọ là 76 ngày.