Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A.
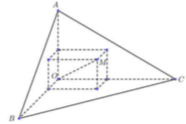
Gọi khoảng cách từ điểm M đến các mặt bên (OAB), (OBC), (OCA) lần lượt là a, b, c.
Khi đó 
Hay 
Thể tích khối gỗ hình hộp chữ nhật theo đề bài là V = abc
Ta có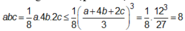 
(Theo bất đẳng thức Cô-sin).
Vậy V = abc đạt giá trị lớn nhất bằng 8( c m 3 ) khi a = 4b = 2c
Chọn B
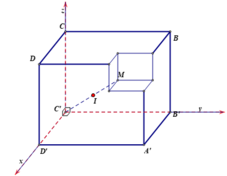
Gọi M là đỉnh của hình lập phương có cạnh bằng 1 nằm trên đường chéo AC' và nằm trên khối còn lại sau khi cắt. Gọi I là tâm của khối cầu có thể tích lớn nhất thỏa yêu cầu bài toán.
Suy ra I thuộc đoạn thẳng C'M và mặt cầu tâm I cần tìm đi qua điểm M
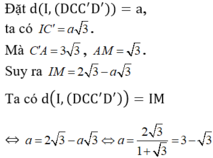
Cách khác: Chọn hệ trục tọa độ Oxyz sao cho C'(0;0;0), B' (0;3;0), D'(3;0;0), C (0;0;3).
Khi đó M(2;2;2)
Ta có phương trình đường thẳng C'M là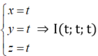 
với 2 > 0 > t do I thuộc đoạn thẳng C'M
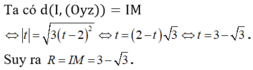
Chọn D.
Thể tích khối gỗ khi chưa bị cắt bớt: V 1 = 5 . 9 . 6 = 270 c m 3
Thể tích phần cắt bớt là: V 2 = 4 3 = 46 c m 3
Thể tích phần còn lại là:
V = V 1 - V 2 = 270 - 64 = 206 c m 3
