Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để khi quạt quay, không một điểm nào trên sàn bị sáng loang loáng thì bóng của đầu mút quạt chỉ in trên tường và tối đa là đến chân tường C và D.
Vì nhà hình hộp vuông, ta chỉ xét trường hơph cho một bóng, các bóng còn lại là tương tự (Xem hình vẽ bên)
Gọi L là đường chéo của trần nhà :
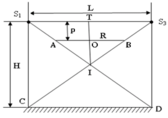
L = 4 2 » 5,7m
Khoảng cách từ bóng đèn đến chân tường đối diện là :
S1D = H 2 + L 2 = ( 3 , 2 ) 2 + ( 4 2 ) 2 = 6 , 5 m
T là điểm treo quạt, O là tân quay của cánh quạt. A, B là các đầu mút khi cánh quạt quay. Xét DS1IS3 ta có :
A B S 1 S 2 = O I I T ⇒ O I = A B S 1 S 2 . I T = 2 R . H 2 L = 2.0 , 8. 3 , 2 2 5 , 7 = 0 , 45 m
Khoảng cách từ quạt đến điểm treo là : OT = IT – OI = 1,6 – 0,45 = 1,15 m.
Vậy quạt phải treo cách trần nhà tối đa là 1,15 m.

k ai giải dc là phải rồi, mk nghĩ bn phải cho bit đường kính bóng đèn, mk làm dc liền



a) Xét tam giác S’IA đồng dạng với tam giác S’I’A’ có:
\(\dfrac{S'I}{S'I'}=\dfrac{IA}{I'A'}=\dfrac{BA}{B'A'}\Rightarrow A'B'=\dfrac{S'I'.BA}{S'I}=\dfrac{S'I+II'}{S'I}.BA\)
mà mà SI = S'I \(\rightarrow\) A'B'= 30cm
b) Để đường kính vệt sáng tăng gấp đôi ta phải di chuyển bóng đèn đến gần gương khi đó
\(\dfrac{A'B'}{AB}=\dfrac{60}{10}=\dfrac{SI+II'}{SI}\rightarrow6SI=SI+II'\rightarrow5SI=II'\)
\(\rightarrow SI=\dfrac{II'}{5}=\dfrac{2}{5}=0,4\left(m\right)=40cm\)
Vậy ta phải dịch bóng đèn lại gần gương một đoạn là:
H = 100 – 40 = 60(cm).
