Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

PTHH: CuO + H2 → Cu + H2O
Số mol của Cu là: 24 : 64 = 0,375 (mol)
Số mol của H2 là: 0,375 mol
Thể tích hiđrô đã dùng là: 0,375 . 22,4 = 8,4 lít
Số mol của CuO là: 0,375 mol
Khối lượng CuO bị khử là: 0,375 . 80 = 30 gam

a) nCu=0,2(mol)
PTHH: CuO + H2 -to-> Cu + H2O
b) nH2=nCuO=nCu=0,2(mol)
=>V(H2,đktc)=0,2.22,4=4,48(l)
c) mCuO=0,2.80=16(g)

Bài 1
\(Fe2O3+3H2-->2Fe+3H2O\)
\(HgO+H2-->Hg+O2\)
\(PbO+H2-->Pb+H2O\)
Bài 2
a)\(Fe2O3+3H2-->2Fe+3H2O\)
\(CuO+H2-->Cu+H2O\)
\(m_{Fe2O3}=20.60\%=12\left(g\right)\)
\(n_{Fe2O3}=\frac{12}{160}=0,075\left(mol\right)\)
\(n_{Fe}=2n_{Fe2O3}=0,15\left(mol\right)\)
\(m_{Fe}=0,15.56=8,4\left(g\right)\)
\(m_{CuO}=20-12=8\left(g\right)\)
\(n_{CuO}=\frac{8}{80}=0,1\left(mol\right)\)
\(n_{Cu}=n_{CuO}=0,1\left(mol\right)\)
\(m_{Cu}=0,1.64=6,4\left(g\right)\)
b)\(n_{H2\left(1\right)}=3n_{Fe2O3}=0,225\left(mol\right)\)
\(n_{H2\left(2\right)}=n_{CuO}=0,1\left(mol\right)\)
\(\sum n_{H2}=0,1+0,225=0,325\left(mol\right)\)
\(V_{H2}=0,325.22,4=7,28\left(l\right)\)
Bài 3
\(2H2+O2-->2H2O\)
\(n_{H2}=\frac{8,4}{22,4}=0,375\left(mol\right)\)
\(n_{O2}=\frac{2,8}{22,4}=0,125\left(mol\right)\)
Lập tỉ lệ
\(n_{H2}\left(\frac{0,375}{2}\right)>n_{O2}\left(\frac{0,125}{1}\right)=>H2dư\)
\(n_{H2O}=2n_{O2}=0,225\left(mol\right)\)
\(m_{H2O}=0,25.18=4,5\left(g\right)\)

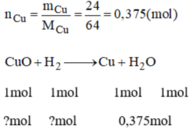
Theo pt: n H 2 = n C u O = 0,375 mol
V H 2 = n H 2 .22,4 = 0,375.22,4 = 8,4(l)
→ Chọn A.

Ta có: \(n_{Cu}=\dfrac{24}{64}=0,375\left(mol\right)\)
\(pthh:CuO+H_2\overset{t^o}{--->}Cu+H_2O\)
Theo pt: \(n_{CuO}=n_{Cu}=0,375\left(mol\right)\)
\(\Rightarrow m_{CuO_{giả.thuyết}}=0,375.80=30\left(g\right)\)
\(\Rightarrow m_{CuO_{thực.tế}}=30:75\%=40\left(g\right)\)
Chọn A
Người ta điều chế được 24 gam đồng bằng cách cho hidro phản ứng với đồng (II) oxit. Khối lượng đồng (II) oxit đã phản ứng là bao nhiêu biết hiệu suất phản ứng là 75%
A. 40 Gam B. 50 Gam
C. 45 Gam D. 20 Gam

\(n_{H_2}=\dfrac{0,65}{22,4}=0,029mol\)
\(CuO+H_2\rightarrow\left(t^o\right)Cu+H_2O\)
0,29 0,29 0,29 ( mol )
\(m_{Cu}=0,29.64=18,56g\)
\(m_{CuO}=0,29.80=23,2g\)

Bài 1.
\(n_{CuO}=\dfrac{48}{80}=0,6mol\)
\(CuO+H_2\rightarrow\left(t^o\right)Cu+H_2O\)
0,6 0,6 0,6 ( mol )
\(m_{Cu}=0,6.64=38,4g\)
\(V_{H_2}=0,6.22,4=13,44l\)
Bài 2.
\(n_{H_2}=\dfrac{5,6}{22,4}=0,25mol\)
\(Fe+2HCl\rightarrow FeCl_2+H_2\)
0,25 0,5 0,25 ( mol )
\(m_{Fe}=0,25.56=14g\)
\(m_{HCl}=0,5.36,5=18,25g\)

\(n_{Cu}=\dfrac{24}{64}=0,375\left(mol\right)\)
PTHH: CuO + H2 --to--> Cu + H2O
0,375<-----------0,375
=> \(m_{CuO\left(PTHH\right)}=0,375.80=30\left(g\right)\)
=> \(m_{CuO\left(tt\right)}=\dfrac{30.100}{75}=40\left(g\right)\)
=> B
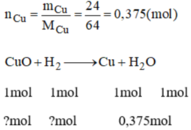
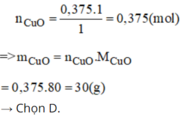
nCu = \(\dfrac{24}{64}=0,375\left(mol\right)\)
Pt: CuO + H2 --to--> Cu + H2O
0,375 mol<----------0,375 mol
mCuO pứ = 0,375 . 80 = 30 (g)
\(CuO+H_2\underrightarrow{t^0}Cu+H_2O\)
\(n_{Cu}=\dfrac{m}{M}=\dfrac{24}{64}=0,375\left(mol\right)\)
Theo PTHH : \(n_{CuO}=n_{Cu}=0,375\left(mol\right)\)
\(\Rightarrow m_{CuO}=n.M=0,375.80=30\left(g\right)\)