Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em thấy bạn Vuông nói đúng
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:

\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh

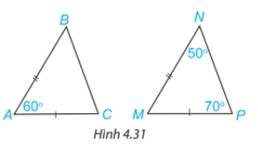
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

Xét tam giác MNP có:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = {180^o}\\ \Rightarrow \widehat M + {50^o} + {70^o} = {180^o}\\ \Rightarrow \widehat M = {60^o}\end{array}\)
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP} (=60^0)\)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

Đoạn thẳng đơn vị được chia thành 6 phần bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng \(\frac{1}{6}\) đơn vị cũ.
Điểm A nằm bên phải gốc O và cách O một đoạn bằng 10 đơn vị mới. Do đó điểm A biểu diễn số hữu tỉ \(\frac{{10}}{6} = \frac{5}{3}\)
Điểm B nằm bên trái gốc O và cách O một đoạn bằng 5 đơn vị mới. Do đó điểm B biểu diễn số hữu tỉ \(\frac{{ - 5}}{6}\)
Điểm C nằm bên trái gốc O và cách O một đoạn bằng 13 đơn vị mới. Do đó điểm C biểu diễn số hữu tỉ \(\frac{{ - 13}}{6}\)

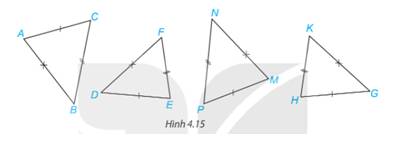
Xét \(\Delta ABC\) và \(\Delta MNP\) có:
\(\begin{array}{l}AB = MN\\BC = NP\\AC = MP\end{array}\)
Vậy\(\Delta ABC\) =\(\Delta MNP\)(c.c.c)
Xét \(\Delta DEF\) và \(\Delta GHK\) có:
\(\begin{array}{l}DE = GH\\EF = HK\\DF = GK\end{array}\)
Vậy\(\Delta DEF\)=\(\Delta GHK\) (c.c.c)

Tham khảo:

a) Vẽ 3 tam giác và xác định điểm O là giao điểm của 3 đường trung trực của 3 cạnh trong tam giác. Khi đó, O cách đều 3 đỉnh của tam giác
b) + Khi tam giác ABC nhọn, điểm O nằm trong tam giác.
+ Khi tam giác ABC vuông, điểm O nằm trên cạnh huyền.
+ Khi tam giác ABC tù, điểm O nằm ngoài tam giác.

Ta có: \(\frac{{33}}{{12}} = \frac{{165}}{{60}};\frac{{79}}{{30}} = \frac{{158}}{{60}}\)
Vì 158 < 165 nên \(\frac{{158}}{{60}} < \frac{{165}}{{60}}\) hay 0 < \(\frac{{79}}{{30}} < \frac{{33}}{{12}}\)
Vì \( - \frac{{25}}{{12}} < - 1\) và \( - 1 < - \frac{5}{6}\) nên \( - \frac{{25}}{{12}} < - \frac{5}{6} < 0\)
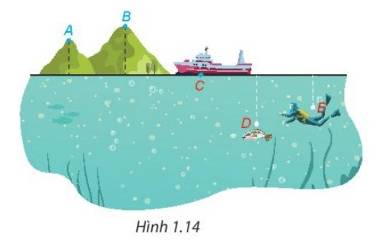
Như vậy, độ cao của:
Điểm D: \( - \frac{{25}}{{12}}\) (km)
Điểm E: \( - \frac{5}{6}\) (km)
Điểm C: 0 (km)
Điểm A: \(\frac{{79}}{{30}}\) (km)
Điểm B: \(\frac{{33}}{{12}}\) (km)

2 góc kề bù trong hình là: góc mOt và tOn
Ta có:
\(\begin{array}{l}\widehat {mOt} + \widehat {tOn} = 180^\circ \\\widehat {mOt} = 180^\circ - \widehat {tOn} = 180^\circ - 60^\circ = 120^\circ \end{array}\)






Ba góc tại mỗi đỉnh chung của ba tam giác tạo thành góc bẹt
Do đó, tổng của chúng bằng 180 độ.
Ta thấy ba điểm A, B, C thẳng hàng.