
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



e hk tham gia
tui đây nè-_-
tui dag nhắn mà ông bơ tui luôn
chán thấy mẹ
ông bỏ rơi tui mà còn kiu nữa
mấy nay buồn thấy mẹ

a)tan (2x+1)*tan (3x-1)=1
\(\Rightarrow\frac{sin\left(2x+1\right)}{cos\left(2x+1\right)}\cdot\frac{sin\left(3x-1\right)}{cos\left(2x-1\right)}=1\)
\(\Rightarrow cos5xcos\left(2-x\right)-cos5x=cos5x+cos\left(2-x\right)\)
\(\Rightarrow2cos5x=0\)
\(\Rightarrow x=\frac{\pi}{10}+\frac{k\pi}{5}\)
b)Đk:\(cosx\ne0,cos\left(x+\frac{\pi}{4}\right)\)
\(pt\Leftrightarrow tanx+\frac{1+tanx}{1-tanx}=1\)
\(\Leftrightarrow tanx\left(1-tanx\right)+1+tanx=1-tanx\)
\(\Leftrightarrow tanx\cdot\left(1-tanx\right)+2tanx=0\)
\(\Leftrightarrow tanx\left(1-tanx+2\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}tanx=0\\tanx=3\end{array}\right.\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=k\pi\\x=a+k\pi\left(a=arctan3\right)\end{array}\right.\)

cau 12:
gọi E là trung điểm AB \(\Rightarrow\)MẸ//BC ; và EN// AC do do ME=BD/2 ;NE= AC/2
\(\Rightarrow\left[\widehat{BD;AC}\right]=\left[\widehat{ME;EN}\right]=90^0\)
\(\Delta MEN\)vuông tại E\(\Rightarrow MN^2=ME^2+NE^2=\left(\dfrac{3a}{2}\right)^2+\left(\dfrac{a}{2}\right)^2=\left(\dfrac{10a^2}{4}\right)\Rightarrow MN=\dfrac{a\sqrt{10}}{2}\)
chọn đáp án A
vẽ hình ở ngoài rồi dán vào ko biết tại sao nó lại thụt xuống dưới![]()

2 : cho ab=cd(a,b,c,d≠0)ab=cd(a,b,c,d≠0) và đôi 1 khác nhau, khác đôi nhau
Chứng minh :
a) C1: Đặt \(\frac{a}{b}=\frac{c}{d}=k\)\(\Rightarrow\left\{{}\begin{matrix}a=kb\\c=kd\end{matrix}\right.\)
\(\frac{a-b}{a+b}=\frac{kb-b}{kb+b}=\frac{b\left(k-1\right)}{b\left(k+1\right)}=\frac{k-1}{k+1}\)
\(\frac{c-d}{c+d}=\frac{kd-d}{kd+d}=\frac{d\left(k-1\right)}{d\left(k+1\right)}\frac{k-1}{k+1}\)
Bài 1:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{\dfrac{3}{2}}=\dfrac{z}{\dfrac{4}{3}}=\dfrac{x-y}{2-\dfrac{3}{2}}=\dfrac{15}{\dfrac{1}{2}}=30\)
Do đó: x=60; y=45; z=40
b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}=\dfrac{x+y+z}{10+15+21}=\dfrac{92}{46}=2\)
Do đó: x=20; y=30; z=42

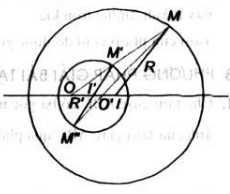
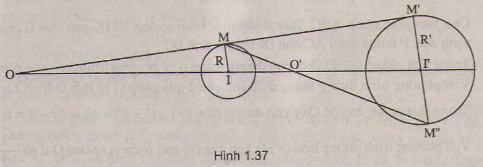
Lấy điểm M thuộc đường tròn (I). Qua I' kẻ đường thẳng song song với IM, đường thẳng này cắt đường tròn (I') tại M' và M''. Hai đường thẳng MM' và MM'' cắt đường thẳng II' theo thứ tự O và O'. Khi đó, O và O' là các tâm vị tự cần tìm
Vì hai đường tròn đã cho có bán kính khác nhau nên chúng có hai tâm vị tự là O và O', xác định trong từng trường hợp như sau ( xem hình vẽ):
a) Trường hợp 1:
b) Trường hợp 2:
c) Trường hợp 3:






 . Tính
. Tính 

 .
. . Tính
. Tính  bằng:
bằng:
 bằng:
bằng:

 .
.



Đáp án A
Tìm điều kiện để phương trình ban đầu có nghĩa. Giải trực tiếp phương trình đã cho và đối chiếu điều kiện để suy ra nghiệm cần tìm.
Điều kiện
Ta có
Đối chiếu với điều kiện
Khi đó
Từ
Do vế phải của biểu thức trên không là số nguyên nó luôn đúng.
Vậy nghiệm của phương trình