Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) + Hàm số y = cos x có chu kì 2π.
Do đó: cos 2.(x + kπ) = cos (2x + k2π) = cos 2x.
⇒ Hàm số y = cos 2x cũng tuần hoàn với chu kì π.
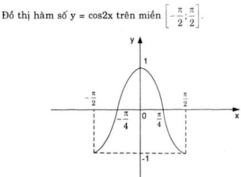
Từ đó suy ra
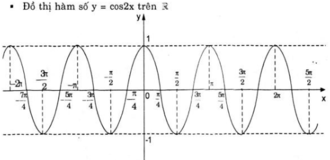
b. y = f(x) = cos 2x
⇒ y’ = f’(x) = (cos 2x)’ = -(2x)’.sin 2x = -2.sin 2x.
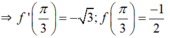
⇒ Phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = π/3 là:
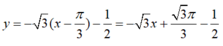
c. Ta có: 1 – cos 2x = 2.sin2x ≥ 0.
Và 1 + cos22x > 0; ∀ x
⇒ 
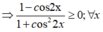
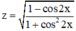luôn xác định với mọi x ∈ R.
Nhận thấy \(cosx-0\) không phải nghiệm, chia 2 vế cho \(cos^2x\)
\(tan^2x+\left(\sqrt{3}-1\right)tanx-\sqrt{3}=0\)
\(\Rightarrow\left[{}\begin{matrix}tanx=1\\tanx=-\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+k\pi\\x=-\frac{\pi}{3}+k\pi\end{matrix}\right.\)
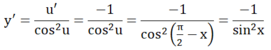
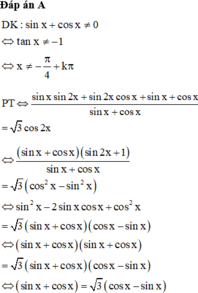
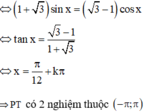
Chọn A
Ta có: - sin 3 x + cos 3 x = sin x – cos x
⇔ ( c os x- sin x) . ( c os 2 x + c osx. sin x+sin 2 x ) + ( c os x - sin x) = 0 ⇔ ( c os x- sin x) . ( 1 + c osx. sin x ) + ( c os x - sin x) = 0 ⇔ ( c osx - sin x ). (1+ c os x. sinx + 1 ) = 0 ⇔ ( c osx - sin x ). (2+ sin 2 x 2 ) = 0 ⇔ cosx - sinx = 0 sin 2 x 2 = − 2
cosx - sin x =0 ⇔ 2 cos x + π 4 = 0 ⇔ cos x + π 4 = 0 ⇔ x + π 4 = π 2 + k π ⇔ x = π 4 + k π
sin 2 x 2 = − 2 ⇔ sin 2 x = − 4 < − 1 n ê n l o ạ i
Vậy nghiệm của phương trình đã cho là: x = π 4 + k π