
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tính chất giao hoán: \(a.b = b.a.\)
Tính chất kết hợp: \((a.b).c = a.(b.c).\)
Nhân với số 1: \(a.1 = 1.a = a\).
Tính chất phân phối của phép nhân đối với phép cộng: \(a.(b + c) = a.b + a.c.\)

Đa thức 3x2 – 8x +1 có các hạng tử là: 3x2 ; -8x ; 1
Ta có: 2x . 3x2 = (2.3). (x.x2) = 6x3
2x. (-8x) = [2.(-8) ]. (x.x) = -16x2
2x. 1 = 2x
Vậy 2x.(3x2 – 8x + 1) = 6x3 -16x2 + 2x

Nêu rõ các bước tính. Ý nghĩa của số trung bình cộng. Khi nào thì số trung bình cộng khó có thể là đại diện của dấu hiệu đó?
Để tính số trung bình cộng của các giá trị của dấu hiệu (nếu số đơn vị điều tra khá lớn) ta lập thêm trong bảng tần số một cột (dòng) ghi các tích mỗi giá trị nhân với tần số tương ứng của chúng.
- Tính tổng các số cột (dòng) tích
- Lấy tổng vừa tính được ở trên chia cho N.
Công thức tính số trung bình cộng:
Ý nghĩa: Số trung bình cộng thường được dùng làm "đại diện" cho dấu hiệu, đặc biệt là khi muốn so sánh các dấu hiệu cùng loại.
Nếu trong dãy các giá trị của dấu hiệu có những giá trị có khoảng cách chênh lệch khá lớn thì lấy số trung bình cộng làm giá trị đại diện cho dấu hiệu không có ý nghĩa thực tế
* Ta có thể tính số TBC của 1 dấu hiệu ( gọi tắt là số TBC của kí hiệu là \(\overline{X}\) ) như sau :
- Nhân từng giá trị với tần số tương ứng.
- Cộng tất cả các tích vừa tìm được
- Chia tổng đó cho số các giá trị ( tức tổng các tần số )
* Ý nghĩa : Số TBC thường đc dùng làm "đại diện" cho dấu hiệu, đặc điểm là khi muốn so sánh các dấu hiệu cùng loại.
Chú ý : Khi các giá trị của dấu hiệu có khoảng cách chênh lệch rất lớn đối với nhau thì ko nên lấy số TBC làm "đại diện" cho dấu hiệu.

17 . 4 = 17. 2 . 2 = 34 . 2 = 68
25 . 28 = 25 . 4 . 7 = 100 . 7 = 700
13 . 12 = 13 . (10 + 2) = 13 . 10 + 13 . 2 = 130 + 26 = 156
53 . 11 = 53 . (10 + 1) = 53 . 10 + 53 = 530 + 53 = 583
39 . 101 = 39 . (100 + 1) = 39 . 100 + 39 = 3900 + 39 = 3939

Ta có : -78 x 31 - 78 x 24 - 78 x 17 + 22 x 72
= 78 x (-31 - 24 - 17) + 22 x 72
= -78 x 72 + 22 x 72
= 72 x (-78 + 22)
= 72 x -56
= -4032

Để tính số trung bình cộng của các giá trị của dấu hiệu (nếu số đơn vị điều tra khá lớn) ta lập thêm trong bảng tần số một cột (dòng) ghi các tích mỗi giá trị nhân với tần số tương ứng của chúng.
- Tính tổng các số cột (dòng) tích
- Lấy tổng vừa tính được ở trên chia cho N.
Công thức tính số trung bình cộng:
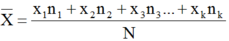 Trong đó:
Trong đó:
x1, x2, ..., xk là k giá trị khác nhau của dấu hiệu x
n1, n2, ..., nk là k tần số tương ứng
N là số các giá trị
Ý nghĩa: Số trung bình cộng thường được dùng làm "đại diện" cho dấu hiệu, đặc biệt là khi muốn so sánh các dấu hiệu cùng loại.
Nếu trong dãy các giá trị của dấu hiệu có những giá trị có khoảng cách chênh lệch khá lớn thì lấy số trung bình cộng làm giá trị đại diện cho dấu hiệu không có ý nghĩa thực tế.
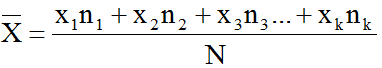
Tính chất giao hoán: \(a + b = b + a.\)
Tính chất kết hợp: \((a + b) + c = a + (b + c).\)
Cộng với số 0: \(a + 0 = 0 + a = a\).
Cộng với số đối: \(a + ( - a) = 0.\)