Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
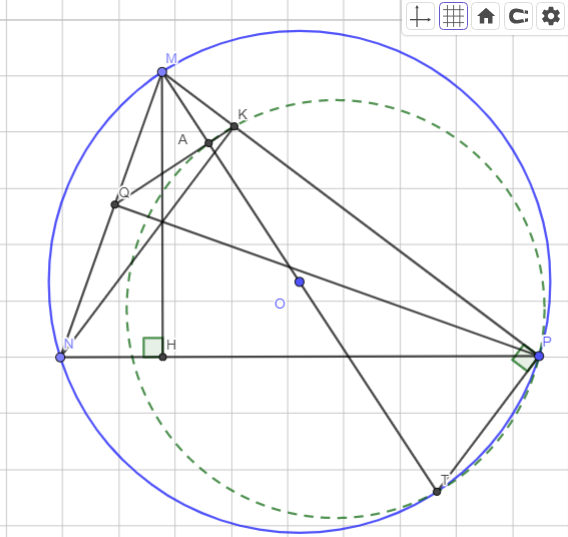
Xét $\Delta MNH$ và $\Delta P$ ta có:
$\large \widehat{MHN}=\widehat{MPT}=90^o$
$\large \widehat{MNP}=\widehat{MTP}$(Hai góc cùng chắn cung $MP$)
Do đó $\large \Delta MNH \sim \Delta MTP$ $(g-g)$
Từ đó: $\frac{MN}{MT}=\frac{MH}{MP}\Leftrightarrow MN.MP=MH.MT$
Xét tứ giác $NQKP$ ta có:
$\large \widehat{NQP}=\widehat{PKN}=90^o$
Mà hai góc này cùng chắn cung $NP$
Do đó tứ giác $NQKP$ là tứ giác nội tiếp
Suy ra: $\large \widehat{PKQ}+\widehat{PNQ}=180^o$ (Hai góc nội tiếp đối nhau)
Đồng thời ta có $\large \widehat{PKQ}+\widehat{MKQ}=180^o\Rightarrow \widehat{MNP}=\widehat{MTP}=\widehat{MKQ}$
Gọi $A$ là giao điểm của $QK$ và $MT$
Xét tứ giác $TPKA$ ta có:
$\large \widehat{MTP}+\widehat{PKQ}=\widehat{PKQ}+\widehat{MKQ}=180^o$
Mà hai góc này ở vị trí đối nhau nên tứ giác $TPAK$ là tứ giác nội tiếp
$\large \Leftrightarrow \widehat{MPT}+\widehat{TAK}=180^o\Leftrightarrow \widehat{TAK}=180^o-\widehat{MPT}=90^o$
Do đó $MT$ vuông góc với $QK$
Hình:
Dạ bài anh có nhầm lẫn gì kh ạ chứ khúc đầu e thấy hơi sai sai 😅😅
Áp dụng định lý Py-ta-go ta có:
\(NP=\sqrt{MP^2-MN^2}\)
\(\Rightarrow NP=\sqrt{10^2-6^2}=8\)
\(\Rightarrow cotM=\dfrac{MN}{NP}=\dfrac{6}{8}=\dfrac{3}{4}=0,75\)
Chọn C
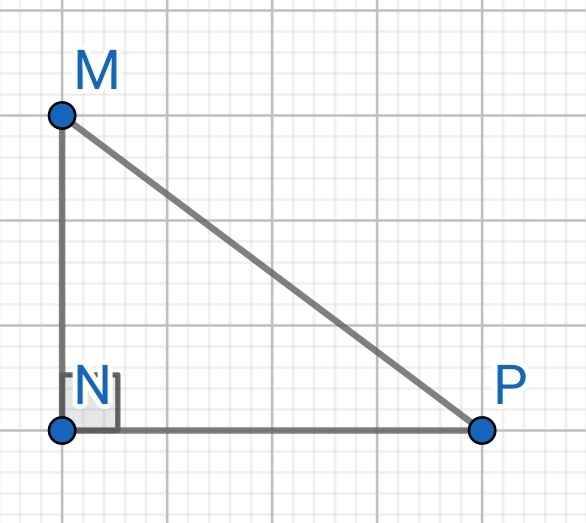∆MNP vuông tại N
⇒ MP² = MN² + NP² (Pytago)
⇒ NP² = MP² - MN²
= 10² - 6²
= 64
⇒ NP = 8 (cm)
⇒ cotM = MN/NP = 6/8 = 0,75
Chọn C
Vì BD và CE là 2 đường trung tuyến => O là giao 2 đường trung tuyến => O là trọng tâm của tam giác => O cách các đỉnh tam giác là \(\frac{2}{3}\)
=> \(\frac{CO}{CE}=\frac{2}{3}=>CO=\frac{4,5.2}{3}=3=>OE=1,5\)
\(TT:BO=4;OD=2\)
=> Diện tích tam giác BEC là 12 \(cm^2\)
NA/BA = NC/BC
Vì Tam giác ABC vuông tại A, biết AB=3cm,BC=5cm => AC= 4(cm)
=> NC-NA=4 (cm)
=> NC/BC = NA/BA = ( NC-NA)/(BC-AB) = 2
=> NA= BA*2 =6 (cm)
\(cot M= \dfrac{MN}{PN}=\dfrac{2}{3}\)