Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Muốn rút gọn phân thức đại số ta có thể :
+ Phân tích tử và mẫu thành nhân tử ( nếu cần ) để tìm nhân tử chung.
+ Chia cả tử và mẫu cho nhân tử chung.
Rút gọn phân thức :
\(\dfrac{8x-4}{8x^3-1}\)\(=\dfrac{4\left(2x-1\right)}{2x^3-1}\)\(=\dfrac{4\left(2x-1\right)}{\left(2x-1\right)\left(2x^2+2x+1\right)}\)\(=\dfrac{4}{4x^2+2x+1}\)
*Quy tắc rút gọn một phân thức đại số là:
-Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung.
-Chia cả tử và mẫu cho nhân tử chung.
*Bài tập:
\(\dfrac{8x-4}{8x^3-1}=\dfrac{4\left(2x-1\right)}{\left(2x-1\right)\left(x^2+x+1\right)}=\dfrac{4}{x^2+x+1}\)

a) x(x-y) + y(x+y) = x^2 - xy + yx + y^2 = x^2 + y^2 = (-6)^2 + 8^2 = 100
b) x(x^2 - y ) - x^2( x + y ) + y(x^2 - x )
= x^3 - xy - x^3 -x^2y+yx^2 - xy
= ( x^3 - x^3 ) + ( x^2 y - x^2 y ) + ( -xy - xy )
= -2xy
Bạn kiểm tra lại đề nhé!

a) ĐKXĐ: \(a^2-1\ne0\Rightarrow\left(a-1\right)\left(a+1\right)\ne0\Rightarrow a\ne\pm1\)
b) ta có \(P=\frac{2a^2}{a^2-1}+\frac{a}{a+1}-\frac{a}{a-1}=\frac{2a^2+a\left(a-1\right)-a\left(a+1\right)}{a^2-1}\)
\(=\frac{2a^2+a^2-a-a^2-a}{a^2-1}=\frac{2a^2-2}{a^2-1}=\frac{2\left(a^2-1\right)}{a^2-1}=2\)

a) phân thức xác định khi \(x^3+8\ne0\Leftrightarrow x^3\ne-8\Leftrightarrow x\ne-2\)
b)\(\frac{2x^2-4x+8}{x^3+8}=\frac{2\left(x^2-2x+4\right)}{\left(x+2\right)\left(x^2-2x+4\right)}=\frac{2}{x+2}\)
c) \(\frac{2}{x+2}=\frac{2}{2+2}=\frac{2}{4}=\frac{1}{2}\)
d)\(\frac{2}{x+2}=2\Leftrightarrow x+2=1\Leftrightarrow x=-1\)

\(A=75\left(4^{1993}+4^{1992}+...+4^2+5\right)+31\)
\(=25\left(4-1\right)\left(4^{1993}+4^{1992}+...+4^2+4+1\right)+31\)
\(=25\left(4^{1994}+4^{1993}+...+4^3+4^2+4-4^{1993}-....-4-1\right)+31\)
\(=25.\left(4^{1994}-1\right)+31\)
\(=25.4^{1994}-25+31\)
\(=25.4^{1994}+6\)
Bài giải
\(A=75\cdot\left(4^{1993}+4^{1992}+...+4^2+4\right)+31\)
Đặt \(B=4^{1993}+4^{1992}+...+4^2+4\)
\(B=4+4^2+...+4^{1992}+4^{1993}\)
\(4B=4^2+4^3+...+4^{1993}+4^{1994}\)
\(4B-B=3B=4^{1994}-4\)
\(B=\frac{4^{1994}-4}{3}\)
Thay \(B=\frac{4^{1994}-4}{3}\) vào biểu thức ta có :
\(A=75\cdot\frac{4^{1994}-4}{3}+31\)
\(B=25\cdot3\cdot\frac{4^{1994}-4}{3}+31\)
\(B=25\cdot\left(4^{1994}-4\right)+31\)

a, \(ĐKXĐ:x^3+8\ne0\Leftrightarrow x\ne-2\)
b, \(C=\frac{2x^2-4x+8}{x^3+8}=\frac{2\left(x^2-2x+4\right)}{\left(x+2\right)\left(x^2-2x+4\right)}=\frac{2}{x+2}\)
c, \(\left|2x+1\right|=3\Rightarrow\orbr{\begin{cases}2x+1=3\\2x+1=-3\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=1\\x=-2\left(ktm\right)\end{cases}\Rightarrow x=1}\)
thay vào ta được : \(C=\frac{2}{1+2}=\frac{2}{3}\)
\(\frac{x}{x+2}=2\Leftrightarrow x=2x+4\)
\(\Leftrightarrow x=-4\left(tm\right)\)
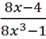
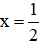 và y = –100;
và y = –100;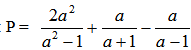
Qui tắc rút gọn một phân thức đại số.
- Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung.
- Chia cả tử và mẫu cho nhân tử chung đó.
Rút gọn: