K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 6 2021
\(I\left(\dfrac{1}{2};\dfrac{3}{4}\right)\)
Nhìn BBT ta thấy \(y_{max}=3\) còn \(y_{min}=\dfrac{3}{4}\)
TV
12 tháng 6 2021
Thầy ơi, tại sao từ đỉnh y mà lại suy ra được Min và max vậy ạ,mong thầy trả lời
)
C
1
8 tháng 10 2023
a: \(=\dfrac{-\dfrac{1}{2}\left[cos\left(a+b+a-b\right)-cos\left(a+b-a+b\right)\right]}{cos^2b-cos^2a}\)
\(=\dfrac{-\dfrac{1}{2}\cdot\left[cos2a-cos2b\right]}{\dfrac{1-cos2b}{2}-\dfrac{1-cos2a}{2}}\)
\(=\dfrac{-\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}{\dfrac{1-cos2b-1+cos2a}{2}}=\dfrac{-\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}{\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}=-1\)
c: \(T=\dfrac{sina+sinb\cdot\left(cosa\cdot cosb-sina\cdot sinb\right)}{cosa-sinb\cdot\left(sina\cdot cosb+sinb\cdot cosa\right)}-tan\left(a+b\right)\)
\(=\dfrac{sina+sinb\cdot cosa\cdot cosb-sin^2b\cdot sina}{cosa-sinb\cdot sina\cdot cosb-sin^2b\cdot cosa}-tan\left(a+b\right)\)
\(=\dfrac{sina\left(1-sin^2b\right)+sinb\cdot cosa\cdot cosb}{cosa\left(1-sin^2b\right)-sinb\cdot sina\cdot cosb}\)-tan(a+b)
\(=\dfrac{sina\cdot cos^2b+sinb\cdot cosa\cdot cosb}{cosa\cdot cos^2b-sinb\cdot sina\cdot cosb}-tan\left(a+b\right)\)
\(=\dfrac{sina\cdot cosb+sinb\cdot cosa}{cosa\cdot cosb-sina\cdot sinb}-tan\left(a+b\right)\)
\(=\dfrac{sin\left(a+b\right)}{cos\left(a+b\right)}-tan\left(a+b\right)=0\)
NT
1
7 tháng 6 2021
\(\dfrac{1}{2}sin6x\ne0\)\(\Leftrightarrow sin6x\ne0\) \(\Leftrightarrow6x\ne k\pi\)\(\Leftrightarrow x\ne\dfrac{k\pi}{6}\)
\(\dfrac{1}{2}\ne0\) rồi nên chỉ cần \(sin6x\ne0\)
HT
28 tháng 12 2020
Gọi số đó có dạng \(\overline{abc}\)
Số lẻ \(\Rightarrow c=\left\{1;3;5;7;9\right\}\) => c có 5 cách chọn
a={1;2;3;4;5;6;7;8;9}=> a có 8 cách chọn
b={0;1;2;3;4;5;6;7;8;9}=> b có 8 cách chọn
=> đáp án của bạn :v
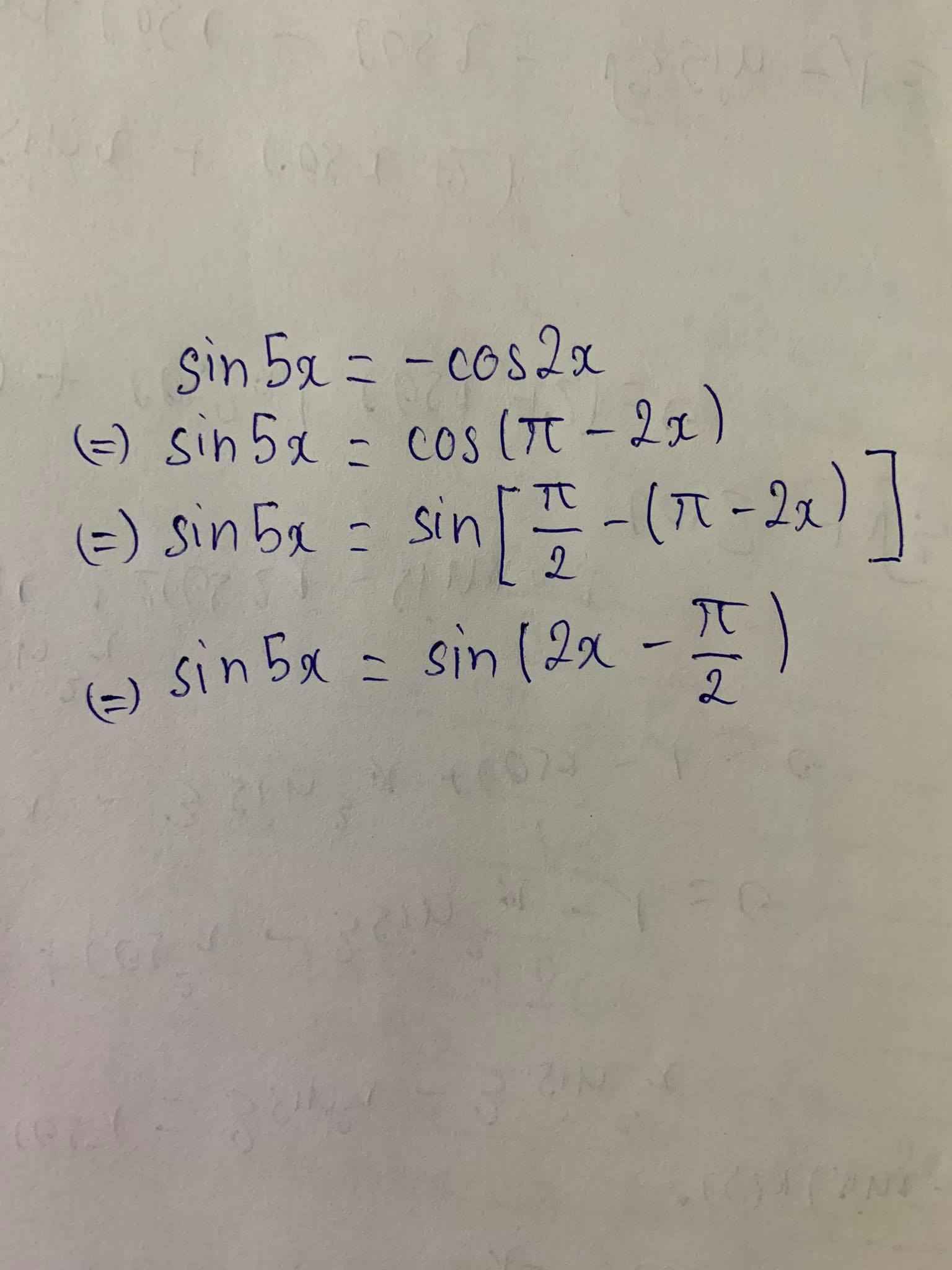
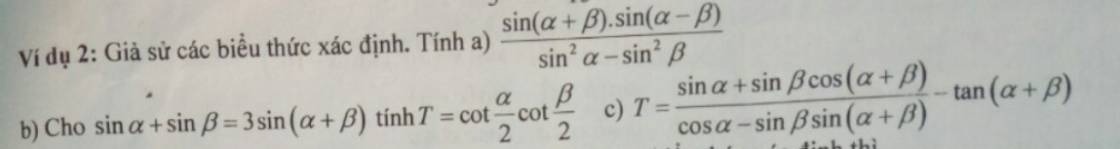
Chọn B
e muốn hỏi tính như trên thì sai chỗ nào ạ