
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2: Gọi số lượng sản phẩm A,B,C công xưởng sản xuất ra lần lượt là a(sản phẩm),b(sản phẩm),c(sản phẩm)
(Điều kiện: a,b,c∈N*)
Số lượng sản phẩm A,B,C lần lượt tỉ lệ với 11;15;22
=>\(\frac{a}{11}=\frac{b}{15}=\frac{c}{22}\)
Tổng số lượng sản phẩm A và sản phẩm B nhiều hơn loại C là 8 sản phẩm nên a+b-c=8
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\frac{a}{11}=\frac{b}{15}=\frac{c}{22}=\frac{a+b-c}{11+15-22}=\frac84=2\)
=>\(\begin{cases}a=2\cdot11=22\\ b=2\cdot15=30\\ c=2\cdot22=44\end{cases}\) (nhận)
Vậy: số lượng sản phẩm A,B,C công xưởng sản xuất ra lần lượt là 22(sản phẩm), 30(sản phẩm), 44(sản phẩm)
1: Gọi số học sinh giỏi Toán, Văn, Anh lần lượt là a(bạn),b(bạn),c(bạn)
(Điều kiện: a,b,c∈N*)
Số học sinh giỏi Toán, Văn, Anh lần lượt tỉ lệ với 2;7;6
=>\(\frac{a}{2}=\frac{b}{7}=\frac{c}{6}\)
Tổng số học sinh giỏi Toán và Văn là 27 bạn nên a+b=27
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\frac{a}{2}=\frac{b}{7}=\frac{c}{6}=\frac{a+b}{2+7}=\frac{27}{9}=3\)
=>\(\begin{cases}a=3\cdot2=6\\ b=3\cdot7=21\\ c=3\cdot6=18\end{cases}\) (nhận)
Vậy: số học sinh giỏi Toán, Văn, Anh lần lượt là 6(bạn), 21(bạn), 18(bạn)

Gọi a,b,c,d lần lượt là số học sinh của 4 khối 6,7,8,9 ( a,b,c,d >0)
Ta có: a/9=b/8=c/7=d/6 và a-c=90
Áp dụng dãy tỉ số bằng nhau:
a/9=b/8=c/7=d/6=a-c/9-7=70/2=35
=> 9=35=> a=9.35=315 học sinh
8=35=> b=8.35=280 học sinh
7=35=> c=7.35=245 học sinh
6=35=> d=6.35=210 học sinh
vậy số học sinh các khối 6,7,8,9 lần lượt là 210 học sinh; 245 học sinh; 280 học sinh; 315 học sinh.

Công thức hai góc kề bù là: tổng số đo của hai góc đó bằng 180 độ. Hai góc kề bù có chung đỉnh và chung một cạnh, đồng thời hai cạnh còn lại là hai tia đối nhau, tạo thành một đường thẳng.
- Có chung đỉnh .
- Có một cạnh chung .
- Hai cạnh còn lại là hai tia đối nhau .

\(\frac{2}{4}=\frac{3}{6}=\frac{2+3}{4+6}\)
\(\frac{2}{4}=\frac{3}{6}=\frac{2-3}{4-6}\)
\(\Rightarrow\frac{2+3}{4+6}=\frac{2-3}{4-6}\)


I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.

Gọi số học sinh của 3 lớp 7A1, 7A2, 7A3 lần lượt là x, y, z (x,y,z nguyên dương)=> x + y + z = 147 (*)
Nếu đưa 1/3 số hs lớp 7A1 đi thi hsg cấp huyện thì số hs còn lại của lớp 7A1 là: x−13xx−13x = 23x23x (học sinh)
Tương tự, số hs còn lại của lớp 7A2 là: y−14y=34yy−14y=34y (học sinh)
Số học sinh còn lại của lớp 7A3 là: z−15z=45zz−15z=45z (học sinh)
Mà theo đề số hs của 3 lớp còn lại = nhau nên:
23x=34y=45z23x=34y=45z ⇒12x18=12y16=12z15⇒12x18=12y16=12z15, ta lại có (*) nên theo tính chất dãy tỉ số bằng nhau ta có:
12x18=12y16=12z
Gọi số học sinh của 3 lớp 7A1, 7A2, 7A3 lần lượt là x, y, z (x,y,z nguyên dương)=> x + y + z = 147 (*)
nếu đưa 1/3 số hs lớp 7A1 đi thi hsg cấp huyện thì số hs còn lại của lớp 7A1 là: x−13xx−13x = 23x23x (học sinh)
Tương tự, số hs còn lại của lớp 7A2 là: y−14y=34yy−14y=34y (học sinh)
số học sinh còn lại của lớp 7A3 là: z−15z=45zz−15z=45z (học sinh)
mà theo đề số hs của 3 lớp còn lại = nhau nên:
23x=34y=45z23x=34y=45z ⇒12x18=12y16=12z15⇒12x18=12y16=12z15, ta lại có (*) nên theo tính chất dãy tỉ số bằng nhau ta có:
12x18=12y16=12z15=12x+12y+12z18+16+15=12(x+y+z)49=12.14749=3612x18=12y16=12z15=12x+12y+12z18+16+15=12(x+y+z)49=12.14749=36
=> x = 36.1812=5436.1812=54
=>y = 36.1612=4836.1612=48
=>z = 36.1512=4536.1512=45
vậy ...
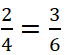
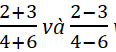 với các tỉ số trong tỉ lệ thức đã cho.
với các tỉ số trong tỉ lệ thức đã cho.
1. Số học & Đại số
\(\frac{a}{b} = \frac{c}{d} \Leftrightarrow a \cdot d = b \cdot c\)
\(\frac{a}{b} = \frac{c}{d} = \frac{e}{f} \Rightarrow \frac{a + c + e}{b + d + f} = \frac{a}{b} = \frac{c}{d} = \frac{e}{f}\)
\(a^{m} \cdot a^{n} = a^{m + n} , \frac{a^{m}}{a^{n}} = a^{m - n} , \left(\right. a^{m} \left.\right)^{n} = a^{m \cdot n}\)
\(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} , \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \left(\right. a , b \geq 0 \left.\right)\)
🔹 2. Hình học phẳng
\(\hat{A} + \hat{B} + \hat{C} = 180^{\circ}\)
\(\text{Trung}\&\text{nbsp};\text{b} \overset{ˋ}{\imath} \text{nh}\&\text{nbsp}; = \frac{1}{2} \cdot \text{c}ạ\text{nh}\&\text{nbsp};đ \overset{ˊ}{\text{a}} \text{y}\)
\(S = \frac{1}{2} \cdot a \cdot h\)
\(S = a \cdot b\)
\(S = a^{2}\)
\(S = \frac{\left(\right. a + b \left.\right) \cdot h}{2}\)
\(S = a \cdot h\)
\(S = \pi R^{2}\)
\(C = 2 \pi R\)
🔹 3. Biểu thức đại số
\(\left(\right. a + b \left.\right)^{2} = a^{2} + 2 a b + b^{2}\) \(\left(\right. a - b \left.\right)^{2} = a^{2} - 2 a b + b^{2}\) \(a^{2} - b^{2} = \left(\right. a - b \left.\right) \left(\right. a + b \left.\right)\)
👉 Đây là những công thức cơ bản lớp 7 thường dùng nhất.
cho mk 1 like bạn nhé