Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A = C = 0 và B ≠ 0 ⇒ mặt phẳng (α) // hoặc trùng với (Oxz)
B = C = 0 và A ≠ 0 ⇒ mặt phẳng (α) // hoặc trùng với (Oyz)


Nên O là tâm đường tròn ngoại tiếp tam giác ABC.
Vậy tam giác ABC có trọng tâm đồng thời là tâm đường tròn ngoại tiếp nên tam giác ABC đều.
Chọn D.

Chọn B.
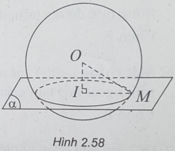
(h.2.58) Gọi I là hình chiếu của O lên ( α ) và M là điểm thuộc đường giao tuyến của ( α ) và mặt cầu S(O;R).
Tam giác OIM vuông tại I, ta có:
OM = R và OI = d
nên 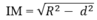

Mặt phẳng ( α ) đi qua điểm D và song song với mặt phẳng (ABC) nên ( α ) cũng có vecto pháp tuyến là n ' → = (1; 1; 1)
Vậy phương trình của ( α ) là: (x – 4) + (y) + (z – 6) = 0 hay x + y + z – 10 = 0.

n → α = (1;-2;3); n → β = (2;-4;6)
Hai vecto pháp tuyến của hai mặt phẳng là hai vecto tỉ lệ



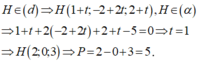
B = 0 ⇒ mặt phẳng (α) // hoặc chứa trục Oy ; C = 0 ⇒ mặt phẳng (α) // hoặc chứa trục Oz