K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TT
3
19 tháng 10 2016
con chó chết với con chuột chết tao là hs đại học đây!
chào chưa
PT
1
AH
Akai Haruma
Giáo viên
29 tháng 12 2023
Lời giải:
Đặt $\frac{a_1}{a_2}=\frac{a_2}{a_3}=\frac{a_3}{a_4}=...=\frac{a_n}{a_{n+1}}=t$
Áp dụng TCDTSBN:
$t=\frac{a_1}{a_2}=\frac{a_2}{a_3}=\frac{a_3}{a_4}=...=\frac{a_n}{a_{n+1}}=\frac{a_1+a_2+a_3+....+a_n}{a_2+a_3+....+a_{n+1}}$
$\Rightarrow t^n=\left[\frac{a_1+a_2+a_3+....+a_n}{a_2+a_3+....+a_{n+1}}\right]^n(*)$
Lại có:
$\frac{a_1}{a_2}.\frac{a_2}{a_3}.\frac{a_3}{a_4}....\frac{a_n}{a_{n+1}}=t.t.t....t$
$\Rightarrow \frac{a_1}{a_{n+1}}=t^n(**)$
Từ $(*)$ và $(**)$ ta có:
$\left[\frac{a_1+a_2+a_3+....+a_n}{a_2+a_3+....+a_{n+1}}\right]^n=\frac{a_1}{a_{n+1}}$ (đpcm)
VH
12 tháng 9 2017
a) Chỉ cần 1 cặp góc so le trong bằng nhau thì tất cả các cặp góc so le trong, so le ngoài đều bằng nhau.
b) Chỉ cần 1 cặp góc so le trong bằng nhau thì tất cả các cặp góc so le trong, so le ngoài, đồng vị, trong cùng phía đều bằng nhau.
12 tháng 9 2017
(minh họa)
a,Giả sử:a//b
Vì A1 và B3 là 2 cặp góc sole ngoài(đề bài)
=>A1=B3(theo tính chất của 2 đường thẳng song song)
b,Nếu có 1 đường thẳng cắt 2 đường thẳng nào đó và tro
Lại có A2 và B4 là 2 cặp góc so le ngoài(đề bài)
=>A2=B4(theo tính chất của 2 đường thẳng song song)
b,Kết luận(phát biểu)
Nếu có 1 đường thẳng cắt 2 đường thẳng nào đó và trong các góc tạo thanh có một cặp góc sole trong,ngoài bằng nhau thì:
+Hai góc còn lại bằng nhau
+2 góc đồng vị bằng nhau
Nếu một đường thẳng cắt 2 đường thẳng song song thì:
-Hai góc sole trong/ngoài bằng nhau
-Hai góc đồng vị bằng nhau
-Hai góc trong cùng phía bằng nhau
NT
2
12 tháng 1 2022
\(\dfrac{a}{b}=\dfrac{b}{c}\Rightarrow ac=b^2\)
\(\dfrac{a^2+b^2}{b^2+c^2}=\dfrac{a^2+ac}{ac+c^2}=\dfrac{a\left(a+c\right)}{c\left(a+c\right)}=\dfrac{a}{c}\)
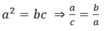
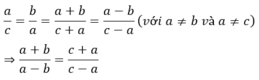
\(\sqrt{a}=4\Leftrightarrow a=16\Rightarrow a^2=256\)
Căn bâc hai của 16 là 4
16 bình phương cằng ...Sorry nha mk ko mang máy tính