Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình
=>MN//AP và MN=AP
=>AMNP là hình bình hành
Xét ΔMNP và ΔPAM có
MN=PA
NP=AM
MP chung
Do đó: ΔMNP=ΔPAM
=>SMNP=SPAM
Xét ΔABC có
M là trung điểm của AB
P là trung điểm của AC
Do đó: MP là đường trung bình
=>MP//BC
Xét ΔABC có MP//BC
nên \(\dfrac{S_{AMP}}{S_{ABC}}=\left(\dfrac{AM}{AB}\right)^2=\dfrac{1}{4}\)
\(\Leftrightarrow S_{AMP}=\dfrac{1}{4}\cdot744=186\left(cm^2\right)\)
hay \(S_{MNP}=186\left(cm^2\right)\)


Diện tích tam giác ABC��� là ::
SΔABC=a×h2=20×122=120(cm2)�Δ���=�×ℎ2=20×122=120(��2)
b,�, Nối A� với M.�. Theo giả thiết ta có ::
SΔABM=12SΔABC=12.120=60cm2�Δ���=12�Δ���=12.120=60��2
SΔMBN=

A B C E I D
1. Ta thấy tam giác DEC Và DBE có chung chiều cao hạ từ đỉnh D mà Đoạn thẳng EC, EB bằng nhau nên Hai tam giác DEC, DEB bằng nhau
Ta thấy tam giác DEI , DAI có chung chiều cao hạ từ đỉnh D mà Đoạn thẳng AI, IE bằng nhau nên Hai tam giác DIA, DIE bằng nhau [1]
Ta thấy hai tam giác AIB, IBE có chung chiều cao hạ từ đỉnh B mà Đoạn thẳng AI, IE bằng nhau nên Hai tam giác ABI, IBE bằng nhau [2]
Từ [1] và [2] => Hai tam giác ABD và DBE bằng nhau mà hai tam giác DBE, DEC bằng nhau
=> Hai tam giác ABD , DEC bằng nhau
=> Tổng diện tích DBE, DEC gấp đôi diện tích tam giác ABD mà hai tam giác có trung chiều cao hạ từ B xuống nên đoạn thẳng DC gấp đôi đoạn thẳng AD.
Ta thấy hai tam giác AEC và AEB có chiều cao hạ từ A xuống mà đoạn thẳng BE và EC bằng nhau nên hai tam giác AEC và AEB bằng nhau
=> Tam giác AEC = 360 : 2 = 180 [cm2 ]
Ta thấy hai tam giác DEC và DEA có chung chiều cao hạ từ E mà đoạn thẳng DC gấp đôi AD
=> Tam giác AED = \(\frac{1}{3}\)tam giác AEC
=> Tam giác AED = \(\frac{1}{3}\) x 180
= 60 [cm2]
Từ [1] ta thấy diện tích tam giác ADI = \(\frac{1}{2}\) tam giác ADE
=>ADI = 60 x \(\frac{1}{2}\)
=> ADI = 30 [cm2]
Vậy diện tích tam giác ADI = 30 cm2
Giải
1)
2)
a) Gọi A là đáy, H là chiều cao
Theo đề bài ta có:
\(\frac{AxH}{2}\) = 72 và \(\frac{A}{12}\) = \(\frac{H}{3}\)
\(\frac{A}{12}\) = \(\frac{Hx4}{3x4}\) = \(\frac{Hx4}{12}\)
Vậy A = H x 4
Thế A vào thì ta có:
\(\frac{Hx4xH}{2}\) = 72
\(Hx4^2\) = 144
\(H^2\) = 144 : 4
\(H^2\) = 36
\(H^2\) = 6 x 6
H = 36
Thế H vào thì ta có:
\(\frac{Ax6}{2}\) = 72
A x 6 = 72 x 2
A x 6 = 144
A = 144 : 6
A = 24
b)
Nối B với N, ta có: S(NBM) = S( NMC). Vì hai tam giác có chung đường cao hạ từ N xuống BC và đáy BM = MC (*).
Theo bài ra MN // AB, nên đường cao hạ từ B xuống MN bằng đường cao hạ từ A xuống MN. Do đó ta có: S( BMN) = S(AMN). Vì hai tam giác có đường cao bằng nhau, đáy MN chung (**)
Từ (*) và (**) ta có: S(AMN) = S(MNC). Vì hai tam giác có diện tích cùng bằng S(BMN).
Do S(AMN) + S(MNC) = S(AMC)
Mà S(AMC) = 1/2 S(ABC). Vì hai tam giác chung đường cao hạ từ A xuống BC, đáy MC = 1/2 BC.
Vậy S(MNC) = 1/4 S(ABC) = 72 : 4 = 18 (cm2).

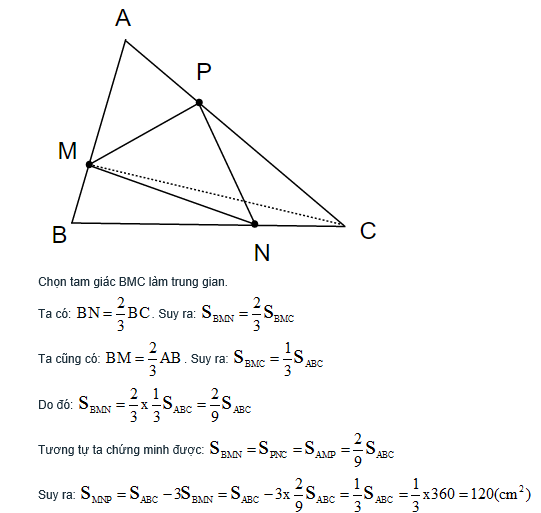
Chọn tam giác BMC làm trung gian. Ta có : Mà Do đó : Tương tự ta chứng minh được Suy ra BN = BC ⇒ = 2 3 SBMN 2 3 SBMC BM = AB ⇒ = 1 3 SBMC 1 3 SABC SBMN = . = 2 3 1 3 SABC 2 9 SABC SBMN = SPNC = SAMP = 2 9 SABC SMNP = SABC − 3SBMN = SABC − 3. = 2 9 SABC 1 3 SAB
k không tui bắng hết

A B C M N P
Nối MC,BP.Từ giả thiết,ta có AM = 2/3 AB ; MB = 1/3 AB ; CP = 2/3 AC ; AP = 1/3 AC ; BN = 2/3 BC ; CN = 1/3 BC
SAPB = 1/3 SABC (vì chung đường cao hạ từ P và có đáy AP = 1/3 AC)
SAPM = 2/3 SAPB = 2/3.1/3 SABC = 2/9 SABC (____________________ P ________ AM = 2/3 AP)
SBMC = 1/3 SABC (____________________ C ________ BM = 1/3 AB)
SBMN = 2/3 SBMC = 2/3.1/3 SABC = 2/9 SABC (____________________ M ________ BN = 2/3 BC)
SBCP = 2/3 SABC (____________________ B ________ CP = 2/3 AC)
SCNP = 1/3 SBCP = 2/3.1/3 SABC = 2/9 SABC (____________________ P ________ CN = 1/3 BC)
=> SMNP = SABC - SAPM - SBMN - SCNP = SABC - 2/9 SABC - 2/9 SABC - 2/9 SABC = 1/3 SABC = 1/3.360 = 120 (cm2)

Tự vẽ hình nha
Diện tích hình tam giác là:
360 :3 x2 =240(cm2)
đáp số:240 cm2
Gọi s là diện tích
Ta có sPMC có diện tích bằng sBMN vì ( BM = MC và có chiều cao bằng nhau)
sABC là: 24 x 62 : 2 = 744 (m2)
sMPCN bằng sAMNP vì có chung PM và có chiều cao bằng nhau => tất cả các tam giác trên hình ABC có diện tích bằng nhau
vậy sMNP = 744 : 4 = 186 (m2)
Đáp số : 186 m2