Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \({u_1} = 97,\;q = \;1 + 0,91\% = 1,0091\).
Dân số của quốc gia sau n năm là: \({u_n} = 97 \times {1,0091^{n - 1}}\).
Dân số của quốc gia năm 2030 tức \(n = 11\) là: \({u_{11}} = 97 \times {1.0091^{11 - 1}} = 106,197\) (triệu người).

Giả sử dân số của quốc gia đó từ năm 2011 đến năm 2021 là dãy số \(\left( {{u_n}} \right)\) với \({u_1} = P\).
Ta có:
\(\begin{array}{l}{u_1} = P\\{u_2} = {u_1} + {u_1}.\frac{a}{{100}} = {u_1}.\left( {1 + \frac{a}{{100}}} \right)\\{u_3} = {u_2} + {u_2}.\frac{a}{{100}} = {u_2}\left( {1 + \frac{a}{{100}}} \right)\\{u_4} = {u_3} + {u_3}.\frac{a}{{100}} = {u_3}\left( {1 + \frac{a}{{100}}} \right)\\ \vdots \\{u_{11}} = {u_{10}} + {u_{10}}.\frac{a}{{100}} = {u_{10}}\left( {1 + \frac{a}{{100}}} \right)\end{array}\)
Vậy dân số các năm từ năm 2011 đến năm 2021 của quốc gia đó tạo thành cấp số nhân với công bội \(q = 1 + \frac{a}{{100}}\).

a) Giả sử dân số của thành phố đó từ năm 2022 là dãy số \(\left( {{u_n}} \right)\) với \({u_1} = 2,1\).
Ta có:
\(\begin{array}{l}{u_1} = 2,1\\{u_2} = {u_1} + {u_1}.\frac{{0,75}}{{100}} = {u_1}.\left( {1 + \frac{{0,75}}{{100}}} \right)\\{u_3} = {u_2} + {u_2}.\frac{{0,75}}{{100}} = {u_2}\left( {1 + \frac{{0,75}}{{100}}} \right)\\{u_4} = {u_3} + {u_3}.\frac{{0,75}}{{100}} = {u_3}\left( {1 + \frac{{0,75}}{{100}}} \right)\\ \vdots \\{u_n} = {u_{n - 1}} + {u_{n - 1}}.\frac{{0,75}}{{100}} = {u_{n - 1}}\left( {1 + \frac{{0,75}}{{100}}} \right)\end{array}\)
Vậy dân số của thành phố đó từ năm 2022 tạo thành cấp số nhân với số hạng đầu \({u_1} = 2,1\) và công bội \(q = 1 + \frac{{0,75}}{{100}}\).
Dân số của thành phố đó vào năm 2032 là: \({u_{11}} = {u_1}.{q^{10}} = 2,1.{\left( {1 + \frac{{0,75}}{{100}}} \right)^{10}} \approx 2,26\) (triệu người).
b) Giả sử sau \(n - 1\) năm thì dân số thành phố đó tăng gấp đôi. Khi đó ta có:
\({u_n} = 2{u_1} \Leftrightarrow {u_1}.{q^{n - 1}} = 2{u_1} \Leftrightarrow {q^{n - 1}} = 2 \Leftrightarrow {\left( {1 + \frac{{0,75}}{{100}}} \right)^{n - 1}} = 2 \Leftrightarrow n \approx 93,77 \Rightarrow n = 94\)
Vậy sau 93 năm thì dân số thành phố đó tăng gấp đôi.
Vậy ước tính vào năm 2115 dân số của thành phố đó sẽ tăng gấp đôi so với năm 2022.

Dân số Việt Nam năm 2030 vào khoảng:
\(S=98564407\cdot e^{0,93\%\cdot9}=107169341\left(người\right)\)

Dân số sẽ gấp đôi dân số của năm lấy làm mốc tính:
\(S=A.e^{r.t}\Rightarrow\dfrac{1}{r}=\ln\dfrac{S}{A}\)
Do \(S_1=2S\Rightarrow t=\dfrac{1}{r}.\ln\dfrac{2S}{S}=\dfrac{1}{r}.\ln2\)

Giả sử số dân của một tỉnh đó hiện nay là N. Vì tỉ lệ tăng dân số là 1,4% nên sau một năm, số dân tăng thêm là 1,4%.N
Vậy số dân của tỉnh đó vào năm sau là
N + 1,4%.N = 101,4%.N = .
Như vậy số dân của tỉnh đó sau mỗi năm lập thành cấp số nhân.
N, ,
, ....
Vậy nếu N = 1,8 triệu người, áp dụng công thức tính số hạng tổng quát của cấp số nhân thì sau 5 năm số dân của tỉnh là ≈ 1,9 (triệu người)
và sau 10 năm sẽ là ≈ 2,1 (triệu người)

Ta có: \({u_1} = 1200,\;d = 30\).
Dân số sau n năm là: \({u_n} = 1200 + 30\left( {n - 1} \right)\)
Vậy dân số của năm 2030 tức \(n = 1\) là: \({u_{11}} = 1200 + 30\left( {11 - 1} \right) = 1500\) (nghìn người).

Giả sử số dân của một tỉnh đó hiện nay là N. Vì tỉ lệ tăng dân số là 1,4% nên sau một năm, số dân tăng thêm là 1,4%.N
Vậy số dân của tỉnh đó vào năm sau là
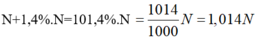
Theo tỷ lệ tăng dân số 1,4% thì dân số hàng năm của tỉnh x là các số hạng của cấp số nhân với công bội q = 1,014
Và số hạng đầu u1 = 1,8 triệu
Theo công thức: un = u1.qn – 1
⇒ Dân số của tỉnh x sau 5 năm sau là:
u6 = 1,8.(1,014)5 ≈ 1.93 triệu (người)
⇒ Dân số sau 10 năm là:
u11 = 1,8.(1,014)10 ≈ 2.07 triệu (người).

Dân số VN năm 2040 là:
\(97.6\cdot\left(1+1.14\%\right)^{20}\simeq122,4\)(triệu người)
Giả sử dân số Việt Nam từ năm 2020 là dãy số \(\left( {{u_n}} \right)\) với \({u_1} = 97,6\).
Ta có:
\(\begin{array}{l}{u_1} = 97,6\\{u_2} = {u_1} + {u_1}.\frac{{1,14}}{{100}} = {u_1}.\left( {1 + \frac{{1,14}}{{100}}} \right)\\{u_3} = {u_2} + {u_2}.\frac{{1,14}}{{100}} = {u_2}\left( {1 + \frac{{1,14}}{{100}}} \right)\\{u_4} = {u_3} + {u_3}.\frac{{1,14}}{{100}} = {u_3}\left( {1 + \frac{{1,14}}{{100}}} \right)\\ \vdots \\{u_n} = {u_{n - 1}} + {u_{n - 1}}.\frac{{1,14}}{{100}} = {u_{n - 1}}\left( {1 + \frac{{1,14}}{{100}}} \right)\end{array}\)
Vậy dân số Việt Nam từ năm 2020 tạo thành cấp số nhân với số hạng đầu \({u_1} = 97,6\) và công bội \(q = 1 + \frac{{1,14}}{{100}}\).
Dân số Việt Nam vào năm 2040 là: \({u_{21}} = {u_1}.{q^{20}} = 97,6.{\left( {1 + \frac{{1,14}}{{100}}} \right)^{20}} \approx 122,4\) (triệu người).
Dân số của nước này sau 20 năm là;
\(A=19\cdot2^{\dfrac{20}{30}}\simeq30\)(triệu người)