Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tính chất 1:
a) Các số có chữ số tận cùng là 0, 1, 5, 6 khi nâng lên lũy thừa bậc bất kì thì chữ số tận cùng vẫn không thay đổi.
b) Các số có chữ số tận cùng là 4, 9 khi nâng lên lũy thừa bậc lẻ thì chữ số tận cùng vẫn không thay đổi.
c) Các số có chữ số tận cùng là 3, 7, 9 khi nâng lên lũy thừa bậc 4n (n thuộc N) thì chữ số tận cùng là 1.
d) Các số có chữ số tận cùng là 2, 4, 8 khi nâng lên lũy thừa bậc 4n (n thuộc N) thì chữ số tận cùng là 6.
Việc chứng minh tính chất trên không khó, xin dành cho bạn đọc. Như vậy, muốn tìm chữ số tận cùng của số tự nhiên x = am, trước hết ta xác định chữ số tận cùng của a.
- Nếu chữ số tận cùng của a là 0, 1, 5, 6 thì x cũng có chữ số tận cùng là 0, 1, 5, 6.
- Nếu chữ số tận cùng của a là 3, 7, 9, vì am = a4n + r = a4n.ar với r = 0, 1, 2, 3 nên từ tính chất 1c => chữ số tận cùng của x chính là chữ số tận cùng của ar.
- Nếu chữ số tận cùng của a là 2, 4, 8, cũng như trường hợp trên, từ tính chất 1d => chữ số tận cùng của x chính là chữ số tận cùng của 6.ar.
Tính chất 2:
Một số tự nhiên bất kì, khi nâng lên lũy thừa bậc 4n + 1 (n thuộc N) thì chữ số tận cùng vẫn không thay đổi.
Chữ số tận cùng của một tổng các lũy thừa được xác định bằng cách tính tổng các chữ số tận cùng của từng lũy thừa trong tổng.

( số cuối - số đầu ) : khoảng cách + 1
Nếu tính tổng thì :
( số cuối + số đầu ) x số số hạng : 2

a^m - a^n = a^m-n .đó là công thức trừ hai số nguyên khác dấu
Muốn trừ số nguyên a cho số nguyên b, ta cộng an với số đối của b
a-b=a+(-b)
tik mik nha, mik tik lại

a) là 1 số nguyên dương
b) ta nhân 2 số như thường (kết quả luôn là số dương)
a) Tích của hai số nguyên âm là một số âm
b) Muốn nhân hai số nguyên khác dấu , ta nhân hai giá trị tuyệt đôi của chúng rồi đặt dấu " - "trước kết quả nhận đc
Tick nha

-
Lũy thừa của 0 và 1[sửa | sửa mã nguồn]
- {\displaystyle 0^{n}=0\,}
.(n > 0)
- {\displaystyle 1^{n}=1\,}
.
Lũy thừa với số mũ nguyên dương[sửa | sửa mã nguồn]
Trong trường hợp b = n là số nguyên dương, lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a:
- {\displaystyle a^{n}=\underbrace {a\times a\cdots \times a} _{n}}
Các tính chất quan trong nhất của lũy thừa với số mũ nguyên dương m, n là
- {\displaystyle a^{m+n}=a^{m}\times a^{n}}
- {\displaystyle a^{m-n}={\frac {a^{m}}{a^{n}}}}
với mọi a ≠ 0
- {\displaystyle (a^{m})^{n}=a^{mn}}
- {\displaystyle a^{m^{n}}=a^{(m^{n})}}
- {\displaystyle (a\times b)^{n}=a^{n}\times b^{n}}
- {\displaystyle ({\frac {a}{b}})^{n}={\frac {a^{n}}{b^{n}}}}
Đặc biệt, ta có:
- {\displaystyle a^{1}=a}
lũy thừa bậc n của a là tích của n thừa số a
các chữ số có tận cùng bằng 5 dều có chũ số tận cùng là 5 nhé
chúc bn hk tốt

ta xem phân số naò có tử lớn hơn thì phân số đó lớn hơn ( bn chỉ dùng cách này khi hai phân số cùng mẫu với nhau thôi nhé )

Qui tắc: Muốn rút gọn một phân số ta chia cả tử và mẫu của chúng cho một ước chung (khác 1 và -1) của chúng.

a: Dãy trên có (86-8)/3+2=78/3+2=28(số)
Tổng là (86+3)*28/2=89*14=1246
b: 32 chia 3 dư 2
=>32 thuộc dãy
47 chia 3 dư 2
=>47 thuộc dãy
54 chia hết cho 3
=>54 không thuộc dãy
c: Số thứ 2011 là u1+2010d=8+2010*3=6038







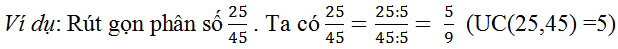
Công thức tính số số hạng của dãy số CÁCH ĐỀU :
( số đầu - số cuối ) : khoảng cách + 1
Công thức tính tổng của dãy số CÁCH ĐỀU :
( số đầu + số cuối ) . số số hạng : 2
Muốn tính số số hạng ta lấy số cuối trừ số đầu chia cho số khoảng cách rồi cộng 1
Muốn tính tổng của dãy ta lấy số đầu cộng số cuối nhân số số hạng rồi chia 2