Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

?1 . Có . Mẫu thức chung : 12x2y3z đơn giản hơn
?2 . \(\dfrac{3}{x^2-5x}=\dfrac{3}{x\left(x-5\right)}=\dfrac{6}{2x\left(x-5\right)}\)
\(\dfrac{5}{2x-10}=\dfrac{5}{2\left(x-5\right)}=\dfrac{5x}{2x\left(x-5\right)}\)
?3 . \(\dfrac{3}{x^2-5x}=\dfrac{3}{x\left(x-5\right)}=\dfrac{6}{2x\left(x-5\right)}\)
\(\dfrac{-5}{10-2x}=\dfrac{5}{2x-10}=\dfrac{5}{2\left(x-5\right)}=\dfrac{5x}{2x\left(x-5\right)}\)

a) Tìm MTC: x3 – 1 = (x – 1)(x2 + x + 1)
Nên MTC = (x – 1)(x2 + x + 1)
Nhân tử phụ:
(x3 – 1) : (x3 – 1) = 1
(x – 1)(x2 + x + 1) : (x2 + x + 1) = x – 1
(x – 1)(x2+ x + 1) : 1 = (x – 1)(x2 + x + 1)
Qui đồng:
b) Tìm MTC: x + 2
2x – 4 = 2(x – 2)
6 – 3x = 3(2 – x)
MTC = 6(x – 2)(x + 2)
Nhân tử phụ:
6(x – 2)(x + 2) : (x + 2) = 6(x – 2)
6(x – 2)(x + 2) : 2(x – 2) = 3(x + 2)
6(x – 2)(x + 2) : -3(x – 2) = -2(x + 2)
Qui đồng:

a) \(\dfrac{3x}{2x+4}\) và \(\dfrac{x+3}{x^2-4}\)
Phân tích các mẫu thức thành nhân tử :
\(2x+4 = 2(x+2)\)
\(x^2 - 4 = (x-2)(x+2)\)
MTC : \(2(x+2)(x-2)\)
Nhân tử phụ của mẫu thức : \(2x + 4\) là \((x - 2)\)
\(x^2 - 4\) là \(2\)
QĐ: \(\dfrac{3x}{2x+4}=\dfrac{3x}{2\left(x+2\right)}=\dfrac{3x\left(x-2\right)}{2\left(x+2\right)\left(x-2\right)}\)
\(\dfrac{x+3}{x^2-4}=\dfrac{x+3}{\left(x+2\right)\left(x-2\right)}=\dfrac{2\left(x+3\right)}{2\left(x+2\right)\left(x-2\right)}\)
b) \(\dfrac{x+5}{x^2+4x+4}\) và \(\dfrac{x}{3x+6}\)
Phân tích các mẫu thức thành nhân tử :
\(x^2+4x+4 = (x+2)^2\)
\(3x + 6\) \(= 3(x+2)\)
MTC : \(3(x+2)^2\)
Nhân tử phụ của mẫu thức : \(x^2 + 4x +4 \) là \(3\)
\(3x + 6\) là \((x+2)\)
QĐ : \(\dfrac{x+5}{x^2+4x+4}=\dfrac{\left(x+5\right)}{\left(x+2\right)^2}=\dfrac{3\left(x+5\right)}{3\left(x+2\right)^2}\)
\(\dfrac{x}{3x+6}=\dfrac{x}{3\left(x+2\right)}=\dfrac{x\left(x+2\right)}{3\left(x+2\right)^2}\)


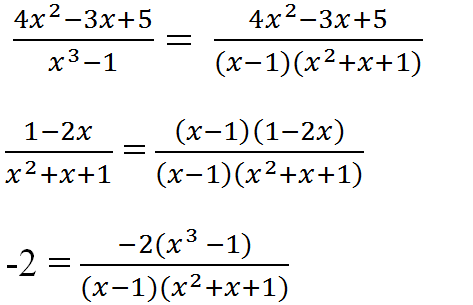
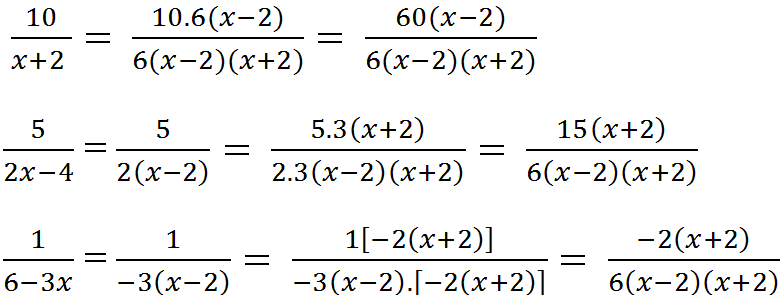
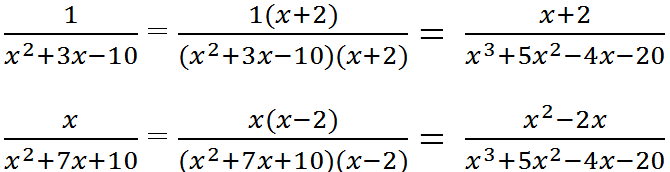
*Muốn quy đồng mẫu thức nhiều phân thức ta làm như sau:
-Phân tích các mẫu thức thành nhân tử rồi tìm ẫu tức chung.
-Tìm nhân tử phụ của mỗi mẫu thức.
-Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.
*Bài tập:
\(\dfrac{x}{x^2+2x+1}và\)\(\dfrac{3}{5x^2-5}\)
-Ta có:
x2+2x+1=(x+1)2=(x+1)(x+1)
5x2-5=5(x2-1)=5(x-1)(x+1)
\(\Rightarrow\)MTC:5(x-1)(x+1)(x+1)
-NTP:5(x-1)(x+1)(x+1):(x+1)(x+1)=5(x-1)
5(x-1)(x+1)(x+1):5(x-1)(x+1)=x+1
-Quy đồng mẫu thức:
\(\dfrac{x}{\left(x+1\right)\left(x+1\right)}\)=\(\dfrac{5x\left(x-1\right)}{5\left(x-1\right)\left(x+1\right)\left(x+1\right)}\)
\(\dfrac{3}{5\left(x-1\right)\left(x+1\right)}=\dfrac{3\left(x+1\right)}{5\left(x-1\right)\left(x+1\right)\left(x+1\right)}\)