Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x (quyển sách) là số quyển sách xưởng in được trong mỗi ngày theo kế hoạch (x ∈ ℕ * )
Số ngày in theo kế hoạch: 6000/x (ngày)
Số quyển sách xưởng in được thực tế trong mỗi ngày: x + 300 (quyển sách)
Số ngày in thực tế: 6000/(x+300) (ngày)
Theo đề bài ta có phương trình:
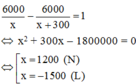
Vậy số quyển sách xưởng in được trong mỗi ngày theo kế hoạch là: 1200 (quyển sách)
Đáp án: D

Gọi x là số sách in được trong 1 ngày theo kế hoạch
\(\Rightarrow\)Số sách in được mỗi ngày để hoàn thành sớm kế hoạch là x+300
\(\Rightarrow\)Thời gian in 6000 quyển sách theo kế hoạch là\(\frac{6000}{x}\)
\(\Rightarrow\)Thời gian in 6000 quyển sách để hoàn thành sớm kế hoạch là\(\frac{6000}{x+300}\)
Ta có phương trình \(\frac{6000}{x}\)=\(\frac{6000}{x+300}\)+1\(\Rightarrow\)x=1200(bạn tự giải phương trình nhé)
\(\Rightarrow\)Số quyển sách xương in được trong 1 ngày theo kế hoạch là 1200 quyển

Gọi x là số quyển sách xưởng in được trong mỗi ngày theo kế hoạch ( x nguyên dương )
Số ngày in theo kế hoạch : 6000/x ( ngày )
Số quyển sách xưởng in được thực tế trong mỗi ngày : x + 300 ( quyển sách )
Số ngày in thực tế : 6000/[x+3]( ngày )
Theo đề bài ta có phương trình : 6000/x -6000/[x+3]= 1
<=> x^2 +300.x 1 800 000 = 0
Giải được : x1 = 1200 [nhận] ; x2 = -1500 [loại]
Vậy số quyển sách xưởng in được mỗi ngày theo kế hoạch là 1200 quyển sách
Gọi x là số quyển sách xưởng in được trong mỗi ngày theo kế hoạch ( x nguyên dương )
Số ngày in theo kế hoạch : 6000/x ( ngày )
Số quyển sách xưởng in được thực tế trong mỗi ngày : x + 300 ( quyển sách )
Số ngày in thực tế : 6000/[x+3]( ngày )
Theo đề bài ta có phương trình : 6000/x -6000/[x+3]= 1
<=> x^2 +300.x 1 800 000 = 0
Giải được : x1 = 1200 [nhận] ; x2 = -1500 [loại]
Vậy số quyển sách xưởng in được mỗi ngày theo kế hoạch là 1200 quyển sách

- Gọi số áo phải may theo kế hoạch trong 1 ngày là x \(\left(x\in N,x>0\right)\)
- Thời gian quy định may xong 3000 áo là \(\frac{3000}{x}\)( ngày )
- Số áo thực tế may được trong 1 ngày là : x + 6 ( áo )
- Thời gian may xong 2650 áo là \(\frac{2650}{x+6}\)( ngày )
- Vì xưởng may xong 2650 áo trước khi hết han 5 ngày nên ta có phương trình :
\(\frac{3000}{x}-5=\frac{2650}{x+6}\)
Giải PT trên :
\(3000\left(x+6\right)-5x\left(x+6\right)=2650x\)hay \(x^2-64x-3600=0\)
\(\Delta'=32^2+3600=4624\); \(\sqrt{\Delta'}=68\)
\(x_1=32+68=100\); \(x_2=32-68=-36\)
\(x_2=-36\left(KTM\right)\)
vậy theo kế hoạch , mỗi ngày xưởng đó phải may xong 100 áo
Gọi số áo mà xưởng may trong một ngày theo kế hoạch là x ( x > 0 )
Số ngày may xong 3000 áo là \(\frac{3000}{x}\)( ngày )
Để hoàn thành sớm kế hoạch, mỗi ngày xưởng đã may thêm nhiều hơn 6 áo
=> Thực tế mỗi xưởng đã may được ( x + 6 ) áo
5 ngày trước khi hết hạn là \(\frac{3000}{x}-5\)( ngày )
Thời gian xưởng may xong 2650 áo là \(\frac{2650}{x+6}\)( ngày )
5 ngày trước khi hết hạn = thời gian xưởng may xong 2650 áo
=> Ta có phương trình :\(\frac{3000}{x}-5=\frac{2650}{x+6}\)
<=> \(\frac{3000}{x}-5-\frac{2650}{x+6}=0\)
<=> \(\frac{3000\left(x+6\right)}{x\left(x+6\right)}-\frac{5x\left(x+6\right)}{x\left(x+6\right)}-\frac{2650x}{x\left(x+6\right)}=0\)
<=> \(\frac{3000x+18000-5x^2-30x-2650x}{x\left(x+6\right)}=0\)
<=> \(\frac{-5x^2+320x+18000}{x\left(x+6\right)}=0\)
=> -5x2 + 320x + 18000 = 0
Δ' = b'2 - ac = 1602 - (-5).18000 = 115 600
Δ' > 0 nên phương trình có hai nghiệm phân biệt :
\(x_1=\frac{-b'+\sqrt{\text{Δ}'}}{a}=\frac{-160+\sqrt{115600}}{-5}=-36\left(loai\right)\)
\(x_2=\frac{-b'-\sqrt{\text{Δ}'}}{a}=\frac{-160-\sqrt{115600}}{-5}=100\left(nhan\right)\)
Vậy theo kế hoạch, mỗi ngày xưởng phải may 100 áo

Bài 1 :
Gọi số người của đội là \(x\) người \(\left(x\inℕ^∗\right)\)
Thời gian làm theo kế hoạch là \(\frac{420}{x}\) ngày
Số người lúc sau là \(x+5\) người
Thời gian hoàn thành lúc sau là \(\frac{420}{x+5}\) ngày
Vì thời gian giảm 7 ngày nên ta có phương trình :
\(\frac{420}{x}-7=\frac{420}{x+5}\)
\(\Leftrightarrow420\left(x+5\right)-7x\left(x+5\right)=420x\)
\(\Leftrightarrow420x+2100-7x^2-35x-420x\)
\(\Leftrightarrow7x^2+35x-2100=0\)
\(\Leftrightarrow x^2+5x-300=0\)
\(\Leftrightarrow\left(x+20\right)\left(x-15\right)=0\)
\(\Leftrightarrow x=15\) \(\left(x\inℕ^∗\right)\)
Vậy số người của đội là 15 người.

Gọi x là sản ppham xưởng sản xuất trong 1 ngày theo kế hoạch (x>0)
=>Số ngày theo kế hoạch là :\(\frac{110}{x}\)
Số ngày thực tế là \(\frac{1100}{x+5}\)theo gia thiet cua bai toan ta co :
\(\frac{1100}{x}-\frac{1100}{x+5}=2\)
<=>1100(x+5)-1100x=2x(x+5)
<=>2x^2+10x-5500=0
<=>x=50hay x=-55 loai
Vậy theo kế hoạch mỗi ngày phân xưởng phải sản xuất là 50 sản phẩm
Gọi số sản phẩm mà phân xưởng làm trong 1 ngày là x ( x > 0 )
=> Số ngày quy định = \(\frac{1100}{x}\)( ngày )
Mỗi ngày phân xưởng sản xuất vượt mức 5 sản phẩm
=> Số ngày hoàn thành = \(\frac{1100}{x+5}\)( ngày )
Vì thế kế hoạch hoàn thành sớm hơn quy định 2 ngày
=> Ta có phương trình : \(\frac{1100}{x}-\frac{1100}{x+5}=2\)
\(\Leftrightarrow\frac{1100\left(x+5\right)}{x\left(x+5\right)}-\frac{1100\cdot x}{x\left(x+5\right)}=\frac{2x\left(x+5\right)}{x\left(x+5\right)}\)
\(\Leftrightarrow1100x+5500-1100x=2x^2+10x\)
\(\Leftrightarrow2x^2+10x-1100x-5500+1100x=0\)
\(\Leftrightarrow2x^2+10x-5500=0\)
\(\Delta'=b'^2-ac=5^2-2\cdot\left(-5500\right)=25+11000=11025\)
\(\Delta'>0\)nên phương trình đã cho có hai nghiệm phân biệt :
\(\hept{\begin{cases}x_1=\frac{-b'+\sqrt{\Delta'}}{a}=\frac{-5+\sqrt{11025}}{2}=50\\x_2=\frac{-b-\sqrt{\Delta'}}{a}=\frac{-5-\sqrt{11025}}{2}=-55\end{cases}}\)
x > 0 => x = 50
Vậy theo kế hoạch , mỗi ngày phân xưởng sản xuất 50 sản phẩm

Gọi số khẩu trang mỗi ngày phải may là x
Theo đề, ta có: 300/x-280/(x+10)=3
=>(300x+3000-280x)/(x^2+10x)=3
=>3x^2+30x=20x+3000
=>x=30
\(\text{# }LQuyen\)
Gọi số sách xưởng in được trong \(1\) ngày là : \(x\) \((x ∈ N ^∗) \)
Số ngày xưởng dự định in hết \(6000\) quyển sách là :
\(\dfrac{6000}{x}\left(ngày\right)\)
Số sách thực tế xưởng in dc trong \(1\) ngày là : \(x+300\) ( quyển sách)
Số ngày xưởng in hết \(6000\) quyển sách với ns thực tế là :
\(\dfrac{6000}{x}-\dfrac{6000}{x+300}=1\)
\(\dfrac{6000\left(x+300\right)-6000x}{x\left(x+300\right)}=1\)
\(\dfrac{1800000}{x\left(x+300\right)}=1\)
\(x^2+300x-1800000=0\)
\((x-1200)(x+1500)=0\)
\(\left[{}\begin{matrix}x=1200\left(tm\right)\\x=-1500\left(loại\right)\end{matrix}\right.\)