Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

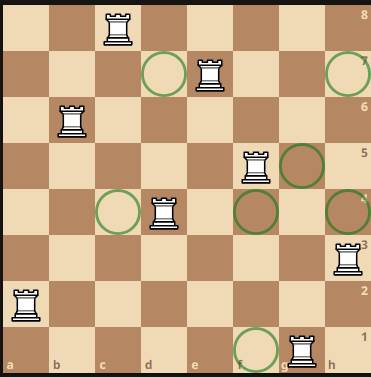
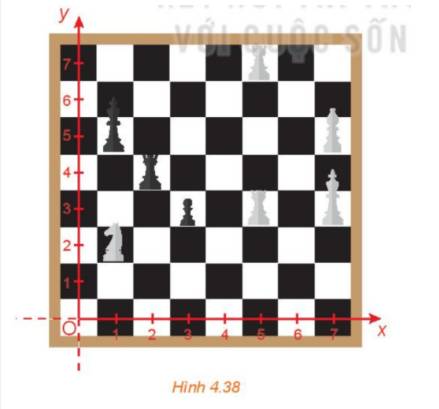
Vị trí của quân xe: hàng 3, cột c
Vị trí của quân mã: hàng 5, cột f

a) Số cách chọn 4 bạn trong 10 bạn nam là: \(C_{10}^4= 210\)
b) Số cách chọn 4 bạn trong tổng 17 bạn (không phân biệt nam, nữ) là: \(C_{17}^4= 2380\)
c) Số cách chọn 4 bạn, trong đó có 2 bạn nam và 2 bạn nữ là: \(C_{10}^2.C_7^2=45. 21= 945\)

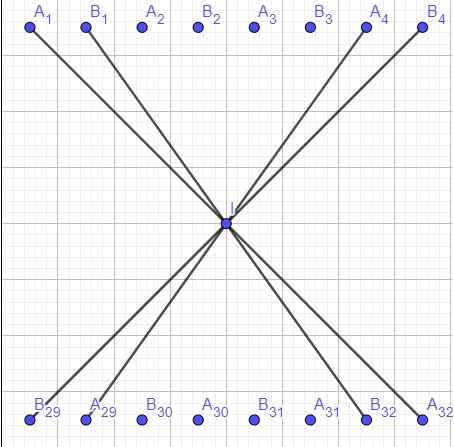
Gọi I là tâm bàn cờ
Khi đó I là trung điểm các đoạn \(A_1A_{32};A_2A_{31}...B_1B_{32};B_2B_{31}...\)
Đồng thời các tứ giác \(A_1B_4A_{32}B_{29};B_1A_4B_{32}A_{29}...\) là các hình chữ nhật nên ta có:
\(IA_1=IB_4;IA_{32}=IB_{29}...\) (1)
Do đó:
\(VT=MA_1^2+MA_2^2+...+MA_{32}^2\)
\(=\left(\overrightarrow{MI}+\overrightarrow{IA_1}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IA_2}\right)^2+...+\left(\overrightarrow{MI}+\overrightarrow{IA_{32}}\right)^2\)
\(=32MI^2+IA_1^2+...+IA_{32}^2+2\left(\overrightarrow{IA_1}+\overrightarrow{IA_{32}}\right)+2\left(\overrightarrow{IA_2}+\overrightarrow{IA_{31}}\right)+...\)
\(=32MI^2+IA_1^2+...+IA_{32}^2\)
Tương tự:
\(VP=32MI^2+IB_1^2+...+IB_{32}^2=VT\) theo (1)

Vì độ chính xác đến hàng trăm (độ chính xác là 0,05) nên ta quy tròn số 41,34 đến hàng phần chục.
Vậy số quy tròn của chiều cao h là 41,3m.
Đáp án C

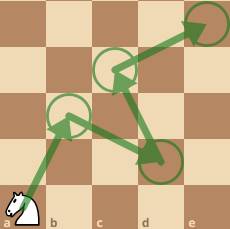
a) Quân mã đi theo đường chéo hình chữ nhật có chiều dài 3 ô, chiều rộng 2 ô.
Do đó, từ vị trí hiện tại, quân mã có thể đi đến các vị trí A, B, C, D, E, F như dưới đây:
A có tọa độ (3; 3)
B có tọa độ (3; 1)
C có tọa độ (2; 0)
D có tọa độ (0; 0)
E có tọa độ (0; 4)
F có tọa độ (2; 4)
Vậy quân mã có thể đi đến các vị trí A(3;3), B(3;1), C(2;0), D(0;0), E(0;4), F(2;4).