Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x(ngày) là số ngày thực tế xí nghiệp hoàn thành công việc sớm hơn và x>0
Ta có: Mỗi ngày xí nghiệp dự định làm 50 sản phẩm.
Nhưng thực tế mỗi ngày xí nghiệp đó làm được 65 sản phẩm.
Số sản phẩm thực tế xí nghiệp đã làm được là 1755 sản phầm.
Ta có phương trình là:
Dự kiến mỗi ngày làm: 1500 : 30 = 50 (sản phẩm).
Thực tế mỗi ngày làm được: 50 + 15 = 65 (sản phẩm).
Số sản phẩm thực tế làm được là: 1500 + 255 = 1755 (sản phẩm).
Số ngày thực tế làm 1755 sản phẩm là: 1755 : 65 = 27 (ngày).
Số ngày rút ngắn so với dự định là: 30 - 27 = 3 ngày.

Theo dự định, mỗi ngày xí nghiệp sản xuất được:
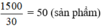
Thực tế, mỗi ngày xí nghiệp sản xuất được:
50 + 15 = 65 (sản phẩm)
Tổng số sản phẩm thực tế xí nghiệm sản xuất được:
1500 + 255 = 1755 (sản phẩm)
Thời gian thực tế xí nghiệm sản xuất là:
1755 : 65 = 27 (ngày)
Vậy số ngày được rút ngắn so với dự định là:
30 – 27 = 3 (ngày).
Gọi số thùng khẩu trang xí nghiệp định sản xuất là x(thùng)
(ĐK: \(x\in Z^+\))
Thời gian dự kiến ban đầu sẽ sản xuất xong là \(\dfrac{x}{30}\left(ngày\right)\)
Số thùng khẩu trang thực tế đã làm được là x+255(thùng)
Thời gian thực tế hoàn thành công việc là \(\dfrac{x+255}{27}\left(ngày\right)\)
Vì mỗi ngày vượt khoảng 15 thùng nên ta có:
\(\dfrac{x+255}{27}-\dfrac{x}{30}=15\)
=>\(\dfrac{x}{27}+\dfrac{85}{9}-\dfrac{x}{30}=15\)
=>\(\dfrac{10x-9x}{270}=15-\dfrac{85}{9}=\dfrac{50}{9}\)
=>\(\dfrac{x}{270}=\dfrac{50}{9}\)
=>\(x=\dfrac{50}{9}\cdot270=1500\left(nhận\right)\)
Vậy: Xí nghiệp dự định sản xuất 1500 thùng