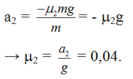Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, đổi 500g = 0,5 kg
vận tốc tại A : v0 , vận tốc tại B: v
Ta có: p = mv => v = p/m = 1/0.5 = 2 m/s
Theo định luật II niu-tơn:
N = P => N =mg => Fms = \(\mu\)mg
Mà -Fms = ma => a = \(\dfrac{-F_{ms}}{m}\)= -1 m/s2
=> v2 - v02 = 2as => v0 = 4 m/s

a. Ta có v A = 72 ( k m / h ) = 20 ( m / s ) ; v B = 18 ( k m / h ) = 5 ( m / s )
Chọn mốc thế năng tại AB
Theo định luật bảo toàn năng lượng W A = W B + A m s
W A = 1 2 m v A 2 = 1 2 .2000.20 2 = 4.10 5 ( J ) W B = 1 2 m v B 2 = 1 2 .2000.5 2 = 25000 ( J ) A m s = μ 1 . m . g . A B = μ 1 .2000.10.100 = 2.10 6 . μ 1 ( J ) ⇒ 4.10 5 = 25000 + 2.10 6 . μ 1 ⇒ μ 1 = 0 , 1875
b. Chọn mốc thế năng tại C
z B = B C . sin 30 0 = 50.0 , 5 = 25 ( m )
Theo định luật bảo toàn năng lượng W B = W C + A m s
W B = 1 2 m v B 2 + m g z B = 1 2 .2000.5 2 + 2000.10.25 = 525000 ( J ) W C = 1 2 m v C 2 = 1 2 .2000. v C 2 = 1000. v C 2 ( J )
A m s = μ 2 . m . g . cos 30 0 . B C = 0 , 1.2000.10. 3 2 .50 = 86602 , 54 ( J ) ⇒ 525000 = 1000 v C 2 + 86602 , 54 ⇒ v C = 20 , 94 ( m / s )

A B C 30 0
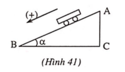
Chọn mốc thế năng tại chân mặt phẳng nghiêng.
a) Cơ năng tại đỉnh mặt phẳng nghiêng
\(W=mgh=mg.AB\sin 30^0=1,2.10.AB.\sin 30^0=24\)
\(\Rightarrow AB = 4(m)\)
b) Tại D động năng bằng 3 lần thế năng, ta có: \(W_đ=3W_t\Rightarrow W = 4W_t \Rightarrow W_t = 24: 4 = 6(J)\)
\(\Rightarrow mgh_1=mg.DB\sin 30^0=1,2.10.DB.\sin 30^0=6\)
\(\Rightarrow DB = 1(m)\)
c) Tại trung điểm mặt phẳng nghiêng
Thế năng: \(W_t = mgh_2=mg.\dfrac{AB}{2}\sin 30^0=1,2.10.2.\sin 30^0=12(J)\)
Động năng: \(W_đ=W-W_t=24-12=12(J)\)
\(\Rightarrow \dfrac{1}{2}.1,2.v^2=12\)
\(\Rightarrow 2\sqrt 5(m/s)\)
d) Công của lực ma sát trên mặt ngang: \(A_{ms}=\mu mg.S\)
Theo định lí động năng: \(W_{đ2}-W_{đ1}=-A_{ms}\Rightarrow 0-24=-\mu.1,2.10.1\Rightarrow \mu = 2\)
anh ơi , anh quên tính vận tốc của vật tại chân mặt phẳng nghiêng kìa . Đãng trí quá .![]()

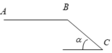
a. Vì Xe chuyển động thẳng đều nên
F = f m s = μ N = μ m g = 0 , 2.2000.10 = 4000 ( N )
b. v C = 72 ( k m / h ) = 20 ( m / s )
Áp dụng định lý động năng
A = W d C − W d B
Công của trọng lực
A P = P x . B C = P sin α . B C = m g sin α . B C A P = 2000.10. 1 2 . B C = 10 4 . B C ( J )
⇒ 10 4 . B C = 1 2 . m . v C 2 − 1 2 m . v B 2 ⇒ 10 4 . B C = 1 2 .2000.20 2 − 1 2 .2000.2 2 ⇒ B C = 39 , 6 ( m )
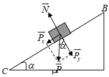
c. Áp dụng định lý động năng
A = W d D − W d C ⇒ A f → m s = 1 2 m v D 2 − 1 2 m v C 2
Công của lực ma sát
A f m s = − f m s . s = − μ N . s = − μ . m g . s / = − μ .2000.10.200 = − μ .4.10 6 ( J )
Dừng lại
v D = 0 ( m / s ) ⇒ − μ 4.10 6 = 0 − 1 2 .2000.20 2 ⇒ μ = 0 , 1

a. Ta có
v A = 18 ( k m / h ) = 5 ( m / s ) ; v B = 54 ( k m / h ) = 15 ( m / s )
Áp dụng định lý động năng
A = 1 2 m v B 2 − 1 2 m v A 2 ⇒ A F → + A f → m s = 1 2 m ( v B 2 − v A 2 )
Mà A f m s = − f m s . s = − μ . N . s = − μ . m . g . s = − 0 , 1.1000.10.100 = − 10 5 ( J ) ⇒ A F → = 1 2 .1000 ( 15 2 − 5 2 ) + 10 5 = 2.10 5 ( J )
b. Ta có
sin α = 60 100 = 3 5 ; cos α = 100 2 − 60 2 100 = 4 5
Áp dụng định lý động năng
A = W d C − W d B ⇒ A P → + A f → m s = 1 2 m v C 2 − 1 2 m v B 2
Công của trọng lực
A P = P x . B C = P sin α . B C = m g sin α . B C A P = 1000.10. 3 5 .100 = 6.10 5 ( J )
Công của lực ma sát
A f m s = − f m s . B C = − μ N . B C = − μ . m g cos α . B C A f m s = − 0 , 1.1000.10. 4 5 .100 = − 8.10 4 ( J )
⇒ 6.10 5 − 8.10 4 = 1 2 .1000. ( v C 2 − 15 2 ) ⇒ v C = 35 , 57 ( m / s )
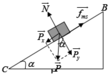
c. Gọi E là vị trí mà xe có thể lên được
v E = 0 ( m / s )
Áp dụng định lý động năng
A = W d E − W d C ⇒ A P → + A f → m s = − 1 2 m v C 2
Công trọng lực của vật
A P → = − P x . C E = − m g sin 30 0 . C E ⇒ A P → = − 1000.10. 1 2 . C E = − 5000. C E ( J )
Công của lực ma sát
A f m s = − f m s . C E = − μ N . C E = − μ . m . g cos 30 0 . C E = − 500 3 . C E ( J )
⇒ − 5000. C E − 500 3 . C E = − 1 2 .1000. ( 35 , 57 ) 2 ⇒ C E = 107 , 8435 ( m ) <...

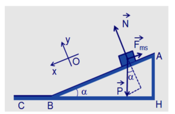
theo định luật II niu tơn trên mặt phẳng nghiêng AB
\(\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m.\overrightarrow{a}\) (1)
chiếu (1) lên trục Ox phương song song với mặt phẳng nằm nghiêng chiều dương cùng chiều chuyển động
\(sin\alpha.P-\mu.N=m.a\) (2)
chiếu (1) lên trục Oy phương vuông gốc với mặt phẳng, chiều dương hướng lên trên
N=\(cos\alpha.P\) (3)
từ (2),(3)
\(\Rightarrow sin\alpha.g-\mu.g.cos\alpha=a\)
\(\Rightarrow a\approx4,1\)m/s2
vận tốc lúc vật tại B
\(v^2-v_0^2=2as_{AB}\Rightarrow v\approx2,875\)m/s

Đáp án: A
Phương trình động lực học:
![]()
Chiếu (1) lên phương song song với mặt phẵng nghiêng (phương chuyển động), chiều dương hướng xuống (cùng chiều chuyển động), ta có:
Psina – Fms = ma1
Chiếu (1) lên phương vuông góc với mặt phẵng nghiêng (vuông góc với phương chuyển động), chiều dương hướng lên, ta có:
N - Pcosa = 0
→ N = Pcosa = mgcosa
→ Fms = m1N = m1mgcosa.
Gia tốc trên mặt phẵng nghiêng:
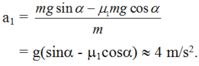
Vận tốc của vật tại B:
![]()
Gia tốc của vật trên mặt phẵng ngang:
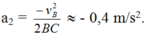
Trên mặt phẵng ngang ta có: