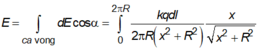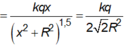Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Điểm phải tìm nằm trong mặt phẳng chứa hai dòng điện, trong khoảng giữa hai dòng điện, cách dòng thứ nhất 30 cm và dòng thứ hai 20 cm. Quỹ tích những điểm ấy là đường thẳng song song với hai dòng điện, cách dòng thứ nhất 30 cm và dòng thứ hai 20 cm.
Điểm phải tìm nằm trong mặt phẳng chứa hai dòng điện, trong khoảng giữa hai dòng điện, cách dòng thứ nhất 30 cm và dòng thứ hai 20 cm. Quỹ tích những điểm ấy là đường thẳng song song với hai dòng điện, cách dòng thứ nhất 30 cm và dòng thứ hai 20 cm.
Ai hok qua lp 11 r lm nhanh
a) Đặt trang sách tại Cck ( điểm cực cận khi đeo kính ) thị kính có ảnh ảo tại Cc do đó :
dc = OCck = 25 cm
d'c = -OCc = - 50 cm
\(\Rightarrow f=\dfrac{d_cd'_c}{d_c+d'_c}=50cm=0,5m\Rightarrow D=\dfrac{1}{f}=2dp\)
b) Ta có :
\(d'_v=-OC_v=-500cm\Rightarrow d_v=\dfrac{d'_cf}{d'_c-f}=45,45cm\)
Vậy khi quẹo kính người đó nhìn được các vật đặt cách mắt 25 đến 45,45 cm .
E=K*Q/r^2 => 1.44r^2=9*10^9*1.6*10^-12 => r^2=0.01 =>r=0.1 =>r=10cm
quỹ tích là các tất cả các điểm nằm trên đường tròn có bk 10 cm
F=kq1q2/r^2 => F=9*10^9*1.6*10^-12*4*10^-12/0.1^2 => F=5.76*10^-12
đáp án D
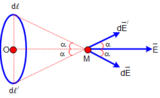
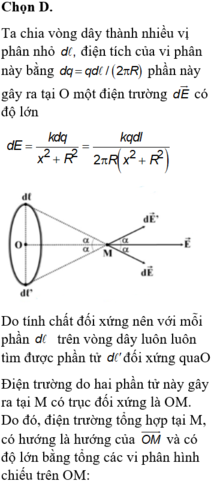
Ta chia vòng dây thành nhiều vi phân nhỏ d ℓ
điện tích của vi phân này bằng d q = q d ℓ 2 π R
phần này gây ra tại O một điện trường d E →
d E = k d q x 2 + R 2 = k q d ℓ 2 π R x 2 + R 2
+ Do tính đối xứng nên với mỗi phần tử d ℓ trên vòng dây luôn luôn tìm được phần tử d ℓ đối xứng với O. Điện trường do hai phần tử này gây ra tại M có trục đối xứng là OM.Do đó, điện trường tổng hợp tại M, có hướng của O M → và có độ lớn bằng tổng các vi phân hình chiếu trên OM
