Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

áp dụng ct: \(p=\dfrac{F}{S}=>\left\{{}\begin{matrix}S1=\dfrac{10m}{p1}\\S2=\dfrac{10m}{p2}\\S3=\dfrac{10m}{p3}\end{matrix}\right.\)\(=>\left\{{}\begin{matrix}S1=\dfrac{20}{1000}=\dfrac{1}{50}m^2\\S2=\dfrac{20}{2000}=\dfrac{1}{100}m^2\\S3=\dfrac{20}{4000}=\dfrac{1}{200}m^2\end{matrix}\right.\)
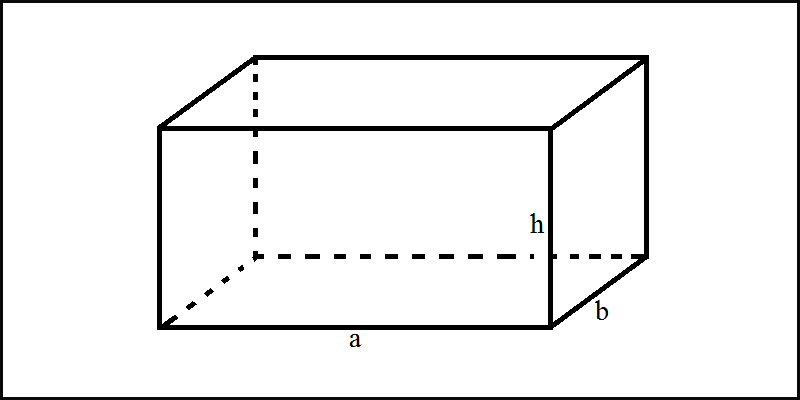
theo hình vẽ \(=>\left\{{}\begin{matrix}a.h=\dfrac{1}{50}\\a.b=\dfrac{1}{100}\\b.h=\dfrac{1}{200}\end{matrix}\right.\)(coi a>h>b)\(=>h=\dfrac{1}{50a},b=\dfrac{1}{100a}=>\dfrac{1}{5000a^2}=\dfrac{1}{200}=>a=0,2m=>h=0,1m,\)
\(=>b=0,05m\)
vậy kích thước: 0,2mx0,1mx0,05m

Đáp án C
- Trọng lượng của viên gạch là:
1,2.10 = 12 (N)
- Áp suất của viên gạch tác dụng lên mặt bàn nhỏ nhất khi diện tíc tiếp xúc lớn nhất.
- Diện tích tiếp xúc lớn nhất là: 20.10 = 200 ( c m 2 ) = 0,02 ( m 2 )
20.10 = 200 ( c m 2 ) = 0,02 ( m 2 )
- Áp suất nhỏ nhất mà viên gạch tác dụng vào mặt bàn là:
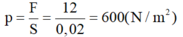

mgạch = 800g=0.8kg=8N
sẽ có 3 trường hợp xãy ra
Trường hợp 1:
Diện tích mặt tiếp xúc có cạnh là 12 và 14 (cm)
S= 12x14= 168(cm2)= 0.0168 m2
=> P=\(\frac{F}{S}=\frac{8}{0.0168}\)=476,2(Pa)
trường hợp 2 mặt tiếp xúc có cạnh lần lượt là 12 và 20 (cm)
S= 12x20= 240 (cm2) =0.024m2
=> P = \(\frac{F}{S}=\frac{8}{0.024}=333.\left(3\right)\left(Pa\right)\)
trường hợp 3, mặt tiếp xúc có cạnh lần lượt là 14 và 20 (cm)
S= 14x20=280(cm2)= 0.028 m2
=> P=\(\frac{F}{S}=\frac{8}{0.028}=285,7\left(Pa\right)\)

Hình như có 3 cách đặt bạn à! Nhưng phải đặt 1 trong 3 cách làm sao để áp suất nhỏ nhất...
Tui cx muốn hỏi câu này
Gọi độ dài các cạnh của viên gạch là a, b, c với a > b > c. Khi đặt viên gạch trên mặt phẳng nằm ngang theo những mặt khác nhau của viên gạch, áp lực tác dụng lên mặt phẳng đều bằng trọng lượng của viên gạch. Do đó diện tích tiếp xúc giữa viên gạch và mặt phẳng càng nhỏ thì áp suất do viên gạch gây ra càng lớn. Theo bài ra ta có:
Pab=1kPa;Pac=2kPa;Pbc=4kPa(1)Pab=1kPa;Pac=2kPa;Pbc=4kPa(1)
Từ đó suy ra : b=a2;c=a4b=a2;c=a4
Thay vào (1) ta được a=0,2m;b=0,1m;c=0,05m