Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
- Xét tại vị trí va chạm thế năng không đổi nên sự biến thiên cơ năng chính là sự biến thiên động năng nó chuyển thành nhiệt tỏa ra khi va chạm.
- Vận tốc của hệ ngay sau va chạm bằng:
- Áp dụng định luật bảo toàn động lượng của hệ khi va chạm mềm
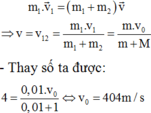
- Ta có công thức giải nhanh trong quá trình va chạm mềm cơ năng của hệ bị giảm. Phần cơ năng giảm này đã chuyển hóa thành nhiệt năng. Nói cách khác ta có công thức nhiệt tỏa ra trong va chạm:
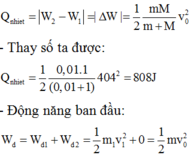
Tỉ lệ phần trăm động năng ban đầu đã chuyển thành nhiệt là:
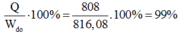
Đáp án C
- Để B có thể dịch sang trái thì lò xo phải giãn một đoạn ít nhất là x0 sao cho:
- Như thế, vận tốc v0 mà hệ (m1 + m) có được ngay sau khi va chạm phải làm cho lò xo có độ co tối đa x sao cho khi nó dãn ra thì độ dãn tối thiểu phải là x0
Ta thấy : \(\left\{{}\begin{matrix}\Sigma\overrightarrow{P_t}=m_1.\overrightarrow{v_1}+m_2\overrightarrow{v_2}=0,5\overrightarrow{v_1}+0,3\overrightarrow{v_2}\\\Sigma\overrightarrow{P_s}=\left(m_1+m_2\right)\overrightarrow{v}=0,8\overrightarrow{v}\end{matrix}\right.\)
- Áp dụng định luật bảo toàn động lượng ta được :
\(0,8\overrightarrow{v}=0,5\overrightarrow{v_1}+0,3\overrightarrow{v_2}\)
Mà \(v,v_1,v_2\) cùng hướng .
\(\Rightarrow0,5v_1+0,3v_2=0,8v\)
\(\Rightarrow v=\dfrac{0,5v_1+0,3v_2}{0,8}=\dfrac{0,5.4+0,3.0}{0,8}=2,5\left(m/s\right)\)
Vậy ...
Chọn chiều chuyển động ban đầu của quả cầu A là chiều dương. Hệ vật gồm hai quả cầu A và B. Gọi v 1 , v 2 và v ' 1 , v ' 2 là vận tốc của hai quả cầu trước và sau khi va chạm.
Vì hệ vật chuyển động không ma sát và ngoại lực tác dụng lên hệ vật (gồm trọng lực và phản lực của máng ngang) đều cân bằng nhau theo phương thẳng đứng, nên tổng động lượng của hệ vật theo phương ngang được bảo toàn (viết theo trị đại số):
m 1 v ' 1 + m 2 v ' 2 = m 1 v 1 + m 2 v 2
2. v ' 1 + 3. v ' 2 = 2.3 +3.1 = 9
Hay v ' 1 + 1,5. v ' 2 = 4,5 ⇒ v ' 2 = 3 - 2 v ' 1 /3 (1)
Đồng thời, tổng động năng của hệ vật cũng bảo toàn, nên ta có:
m1 v ' 1 2 /2 + m2 v ' 2 2 /2 = m1 v 1 2 /2 + m2 v 2 2 /2
2 v ' 1 2 /2 + 3 v ' 2 2 /2 = 2. 3 2 /2 + 3. 1 2 /2
Hay v ' 1 2 + 1,5 v ' 2 2 = 10,5 ⇒ v ' 2 2 = 7 - 2 v ' 1 2 /3 (2)
Giải hệ phương trình (1), (2), ta tìm được: v ' 1 = 0,6 m/s; v ' 2 = 2,6 m/s
(Chú ý: Loại bỏ cặp nghiệm v ' 1 = 3 m/s, v ' 2 = 1 m/s, vì không thỏa mãn điều kiện v ' 2 > v 2 = 1 m/s)
Chọn chiều \(\left(+\right)\) là chiều chuyển động của vật thứ nhất trước va chạm.
Trước va chạm
\(m_1=500g=0,5kg\) \(;\) \(v_1=+4m/s\)
\(m_2=300g=0,3kg\) \(;\) \(v_2=+0\) (Do trước va chạm vật đứng yên)
Sau va chạm
\(M=\left(m_1+m_2\right)=0,5+0,3=0,8kg\)
\(V=?m/s\)
==============================
Vì hệ kín, áp dụng định luật bảo toàn động lượng, ta có :
\(\overrightarrow{p_{trước}}=\overrightarrow{p_{sau}}\)
\(\Rightarrow m_1\overrightarrow{v_1}+m_2\overrightarrow{v_2}=M\overrightarrow{V}\left(1\right)\)
Chiếu \(\left(1\right)\) lên chiều dương là chiều chuyển động của vật được chọn.
\(m_1v_1+m_2v_2=MV\)
\(\Leftrightarrow0,5.4+0,3.0=0,8.V\)
\(\Leftrightarrow0,8V=2\)
\(\Leftrightarrow V=+2,5\left(m/s\right)\)
Dấu \(+\) cho biết sau va chạm hai vật chuyển động cùng chiều chuyển động của vật thứ nhất trước va chạm.
Vậy vận tốc của 2 vật sau va chạm là \(2,5m/s\)
Chọn chiều dương là chiều chuyển động của viên bi một trước lúc va chạm
Theo định luật bảo toàn động lượng
m 1 . v → 1 + m 2 . v → 2 = m 1 . v → 1 ' + m 2 . v → 2 '
a. Sau va chạm hai viên bi đứng yên nên
v 1 ' = v 2 ' = 0 ( m / s )
Chiếu lên chiều dương ta có
m 1 . v 1 − m 2 . v 2 = 0 ⇒ v 2 = m 1 . v 1 m 2 = 4.4 8 = 2 ( m / s )
b. Sau va chạm viên bi hai đứng yên viên bi một chuyển động ngược chiều với vận tốc 3 m/s ta có:
Chiếu lên chiều dương
m 1 . v 1 − m 2 . v 2 = − m 1 . v 1 / + 0 ⇒ v 2 = m 1 . v 1 + m 1 . v 1 / m 2 ⇒ v 2 = 4.4 + 4.3 8 = 3 , 5 ( m / s )
