Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
+ Hai dao động cùng pha![]() và pha φ là pha của các dao động
và pha φ là pha của các dao động
=> x = 15cos(πt + π/6)cm.

Ta có $x_1=x_{12}-x_2=x_{12}-(x_{23}-(x_{13}-x_1)$
$\Rightarrow$ $2x_1=x_{12}-x_{23}+x_{13}$. Bấm máy tính ta được
${x_1}={3\sqrt{6}}\cos\left({\pi t + \dfrac{\pi}{12}} \right)$
${x_3}={3\sqrt{2}}\cos\left({\pi t + \dfrac{7\pi}{12}} \right)$
Suy ra hai dao động vuông pha, như vậy khi x1 đạt giá trị cực đại thì x3 bằng 0.
![]()
cách bấm máy để ra phương trình dao động làm như thế nào vậy ạ

Từ giả thuyết bài toán, ta có:
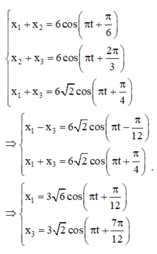
+ Hai dao động này vuông pha nhau. Ta có
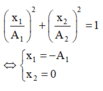
Đáp án A

- Có thể bấm nhanh bằng máy tính:
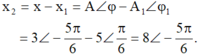
- Vậy dao động thứ 2 có phương trình li độ:
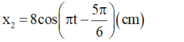

Đáp án B
Phương pháp: Sử dụng lí thuyết về tổng hợp hai dao động điều hòa cùng phương, cùng tần số
Cách giải:
Ta có x = x1 + x2 => x2 = x – x1
x = 3cos(πt - 5π/6) (cm)
x1 = 5cos(πt + π/6) (cm) => - x1 = 5cos(πt - 5π/6)
=> x2 = 8cos(πt - 5π/6) (cm) => Chọn B

Chọn đáp án A
A = 4 2 + 4 2 + 2.4.4. cos − π 6 + π 2
= 4 3 ( c m )

Đáp án D
Phương pháp: Áp dụng công thức tính biên độ của dao động tổng hợp hai dao động cùng tần số.
Cách giải:
Biên độ dao động tổng hợp: A 1 2 + A 2 2 + 2 A 1 A 2 cos ∆ φ ⇒ A 48 = 4 3 c m

Đáp án B
Ta có T = 2π/ω = 2 s và A = 10 cm
Tại t = 0, x = 0 cm; Δt = 1 s = T/2 → ΔS = 2A = 20 cm

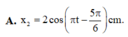
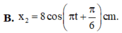
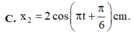
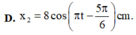
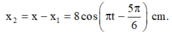
Hướng dẫn: Chọn đáp án D
Đổi hàm sin về hàm
Cách 1:
Cách 2:
x = x 1 + x 2
Cách 3:
Bình luận : Đáp án đúng là A! Vậy cách 1 và cách 2 sai ở đâu? Ta dễ thấy, véc tơ tổng A → = A 1 → + A 2 →
nằm ở góc phần tư thứ III vì vậy không thể lấy φ = - 1 , 51 r a d !
Sai lầm ở chỗ, phương trình có hai nghiệm :
Ta phải chọn nghiệm 1,63 rad để cho véc tơ tổng “bị kẹp” bởi hai véc tơ thành phần. Qua đó ta thấy máy tính không “dính những bẫy” thông thường giống như con người! Đây chính là một trong những lợi thế của cách 3.