K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
11 tháng 4 2019
Đáp án A.
Coi khối lập phương có cạnh 1.
Thể tích khối lập phương là V = 1
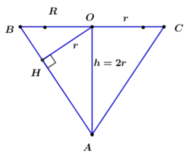
Từ giả thiết ta suy ra khối nón có chiều cao h=1, bán kính đáy r=1/2
Thể tích lượng nước trào ra ngoài là thể tích V1 của khối nón.

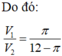

CM
2 tháng 2 2019
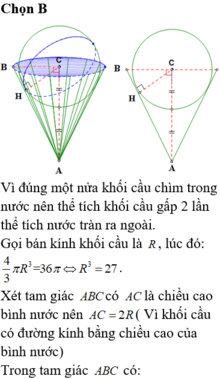
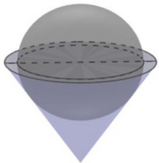
Chọn B
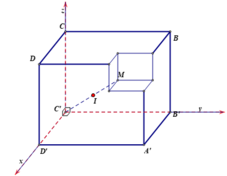
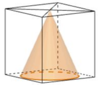
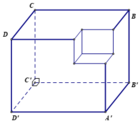
Gọi M là đỉnh của hình lập phương có cạnh bằng 1 nằm trên đường chéo AC' và nằm trên khối còn lại sau khi cắt. Gọi I là tâm của khối cầu có thể tích lớn nhất thỏa yêu cầu bài toán.
![]()
Suy ra I thuộc đoạn thẳng C'M và mặt cầu tâm I cần tìm đi qua điểm M
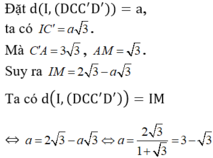
Cách khác: Chọn hệ trục tọa độ Oxyz sao cho C'(0;0;0), B' (0;3;0), D'(3;0;0), C (0;0;3).
Khi đó M(2;2;2)
Ta có phương trình đường thẳng C'M là 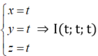 với 2 > 0 > t do I thuộc đoạn thẳng C'M
với 2 > 0 > t do I thuộc đoạn thẳng C'M
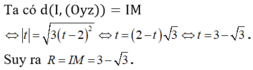

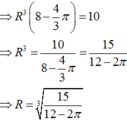







Gọi cạnh của hình lập phương là \(2x\) thì bán kính khối cầu là \(x\)
Thể tích hình lập phương: \(\left(2x\right)^3=8x^3\)
Thể tích khối cầu: \(\frac{4}{3}\pi x^3\)
Ta có pt:
\(8x^3-\frac{4}{3}\pi x^3=10\Rightarrow x=\sqrt[3]{\frac{10}{8-\frac{4}{3}\pi}}\approx1,38\)