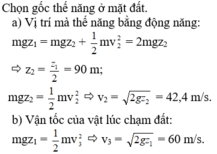Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn mốc thế năng tại mặt đất
Giả sử tại ví trí (2) có \(W_đ=2W_t\)
Theo định luật bảo toàn cơ năng, ta có:
\(W_1=W_2\)
\(\Rightarrow m.g.h_1=W_{đ_2}+W_{t_2}\)
\(\Rightarrow m.g.h_1=2W_{t_2}+W_{t_2}=3W_{t_2}\)
\(\Rightarrow m.g.h_1=3.m.g.h_2\)
\(\Rightarrow120=3.h_2\)
\(\Rightarrow h_2=40\left(m\right)\)
#trannguyenbaoquyen

giải
Chọn mốc thế năng tại mặt đắt, trục 0z hướng lên
Công của vật lúc bắt đầu rơi là :
W=Wt+Wđ=Wt=m.g.z
Vật chỉ chịu tác dụng của trọng lực , nên cơ năng không đổi
Khi:
\(Wđ1=\)\(2\)\(Wt1\)
\(W1=\)\(Wt1+\)\(Wđ1\)
\(\Leftrightarrow m.g.z=3\)\(Wt1\)
\(\Leftrightarrow m.g.z=3.m.g.z_1\)
\(\Leftrightarrow z=3z_1\Rightarrow z_1=40\left(m\right)\)

Chọn mốc thế năng ở mặt đất.
a) Cơ năng của vật ở mặt đất: \(W_1=\dfrac{1}{2}mv_0^2\)
Cơ năng của vật ở độ cao cực đại: \(W_2=mgh\)
Theo định luật bảo toàn cơ năng: \(W_1=W_2\Rightarrow \dfrac{1}{2}mv_0^2=mgh\Rightarrow h = \dfrac{v_0^2}{2g}=\dfrac{30^2}{2.10}=45m\)
b) Vật có \(W_đ=4W_t \Rightarrow W_3=W_đ+W_t=4W_t+W_t=5W_t=5mgh_3\)
Bảo toàn cơ năng ta có: \(W_3=W_2\Rightarrow 5mgh_3=mgh\Rightarrow h_3=\dfrac{h}{3}=\dfrac{45}{3}=15m\)
Mặt khác \(W_đ=4W_t \Rightarrow W_3=W_đ+W_t=W_đ+W_đ/4=5/4W_đ=\dfrac{5}{4}.\dfrac{1}{2}mv_3^2\)
Bảo toàn cơ năng: \(W_3=W_1\Rightarrow v_3=\dfrac{2}{\sqrt 5}v_0=\dfrac{2}{\sqrt 5}.30=12\sqrt 5\)(m/s)
c) Làm tương tự câu b.
ở câu b chỗ tính độ cao 45/3 bạn tính như thế nào ra được 3 thế ạ

chọn gốc thế năng trọng trường ở mặt đất
a,
cơ năng của vật
W= mgh + \(\frac{1}{2}mv^2=0,2.10.3+0,5.0,2.4^2=7,6J\)
b,
độ cao lên được
bảo toàn cơ năng:
\(W=mgh\Rightarrow h=\frac{W}{mg}=\frac{7,6}{0,2.10}=3,8m\)
c,
Tiếp tục bảo toàn cơ năng, khi chạm đất thì thế năng bằng 0
\(W=\frac{1}{2}mv^2\Rightarrow v=2\sqrt{19}m\text{/}s\)
d,
khi động năng = thế năng. cho \(mgh=0,5mv^2=0,5W\Rightarrow h=1,9m\)
từ đó suy ra quãng đường đi được
\(s=3,8-3+3,8-1,9=2,7m\)