Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/ Đáp án B
2/
a) Thời gian vật rơi:
\(t=\frac{v}{g}=3\left(s\right)\)
- Độ cao thả vật:
\(h=\frac{1}{2}gt^2=45\left(m\right)\)
b) Quãng đường vật rơi trong giây cuối cùng trước khi chạm đất :
\(\Delta s'=s_3-s_2=25\left(m\right)\)
1.B
2. a) h=\(\dfrac{v^2}{2g}\)=\(\dfrac{30^2}{2.10}\)=45(m)
t=\(\dfrac{v}{g}\)=\(\dfrac{30}{10}\)=3(s)
b) S2s=\(\dfrac{1}{2}\)gt2s2=\(\dfrac{1}{2}\).10.22=20(m)
\(\Delta S\)=S3s-S2s=h-S2s=25(m)

50cm=0,5m
a)\(\omega\)=\(\dfrac{60.2\pi}{60}\)\(\approx\)6,28(rad/s)
\(f=\dfrac{\omega}{2\pi}\)=1 (Hz)
T=\(\dfrac{1}{f}=1s\)
b)Fht=\(\omega^2.R.m\)\(\approx\)1,973N
c) tại điểm cao nhất Fht=P+T\(\Rightarrow\)T=0,973N
tại điểm thấp nhất Fht=T-P\(\Rightarrow\)T=2,973N

Chọn đáp án B
+ Áp dụng công thức
![]()
![]()
+ Vận tốc dài: ![]()
+ Gia tốc hướng tâm:
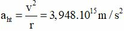

Gọi \(t\left(s\right)\)là thời gian để hai xe đuổi kịp nhau. \(\left(t>0\right)\)
Ta có: \(4t+\frac{1}{2}.0,2t^2=200+1.t+\frac{1}{2}.0,1.t^2\)
\(\Leftrightarrow\frac{1}{20}t^2+3t-200=0\)
\(\Leftrightarrow\orbr{\begin{cases}t=40\left(tm\right)\\t=-100\left(l\right)\end{cases}}\)
Vị trí hai xe gặp nhau cách A quãng đường là: \(4.40+\frac{1}{2}.0,2.40^2=320\left(m\right)\)

\(\overrightarrow{F_{ht}}=m.\overrightarrow{a_{ht}}\Rightarrow F_{ht}=m.a_{ht}\)
\(\overrightarrow{F_{msn}}=\mu.\overrightarrow{N}\Rightarrow F_{msn}=\mu mg\)
Có \(F_{ht}\le F_{msn}\Rightarrow m.a_{ht}\le\mu mg\)
\(\Leftrightarrow\omega^2.R\le\pi^2.\mu\)
\(\Leftrightarrow\pi^2.0,2\le\pi^2.\mu\Rightarrow\mu\ge0,2\)
Vậy để vât ko bị trượt thì \(\mu\ge0,2\)

Hướng dẫn giải:
Gọi mA là khối lượng của xe ca.
mB là khối lượng của xe móc.
Chọn trục Ox nằm ngang, chiều dương là chiều chuyển động.
Định luật II Niu-tơn cho:
a) Hợp lực tác dụng lên xe A chính là hợp lục tác dụng lên hệ (A và B).
Fhl = (mA+mB)a = (1250 +325). 2,15
=> Fhl = 3386,25 N
b) Hợp lực tác dụng lên xe B.
Fhl = mB.a
Fhl = 325. 2,15 = 698,75 N.


Chọn A