Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chu kì: T = 0,5s
Độ lớn của gia tốc: \(|a| = \omega^2|x|\) nên khi khi \(|a| = \frac{a_{max}}{2}\) thì \(x = \pm\frac{A}{2}\)
Biểu diễn bằng véc tơ quay ta có:
M N x 60 0
Ban đầu véc tơ quay xuất phát tại M, thời điểm gần nhất thỏa mãn điều kiện, véc tơ quay đến N, góc quay 600
Thời gian: \(t = \frac{60}{360}T = \frac{T}{6}\)=0,5/6 = 0,083s

\(\left|v\right|>\frac{\sqrt{3}}{2}v_{max}\Rightarrow\left[{}\begin{matrix}v>\frac{\sqrt{3}}{2}v_{max}\\v< -\frac{\sqrt{3}}{2}v_{max}\end{matrix}\right.\)
\(\Delta t=\frac{0,5}{4}=\frac{1}{8}\left(s\right)\) ;\(\Delta t=\frac{1}{\omega}arc\cos\left(\frac{\sqrt{3}}{2}\right)\Rightarrow\omega=\frac{4}{3}\pi\left(rad/s\right)\)
\(a_{max}=\omega^2A=\frac{160}{9}\pi^2\left(cm/s^2\right)\)
Tại thời điểm t=0, gia tốc của vật là: \(a=-\omega^2A\cos\frac{\pi}{3}=-\frac{160}{9}\pi^2.\frac{1}{2}\left(cm/s^2\right)\)
\(\Rightarrow a=-\frac{1}{2}a_{max}\)
\(\Rightarrow\Delta t_1=\frac{1}{\omega}arc\sin\left(\frac{1}{2}\right)=\frac{3}{4\pi}.\frac{\pi}{6}=\frac{1}{8}\left(s\right)\)
\(\Delta t_2=\frac{T}{4}=\frac{3}{2.4}=\frac{3}{8}\left(s\right)\)
\(\Rightarrow\Delta t=t_1+t_2=....\)
P/s: Check lại số má giùm em nha :)

+ Từ phương trình v = 10 π c os 2 π t + 0 , 5 π = ω A cos 2 π t + φ + π 2
® x = 5 cos 2 π t .
® Quỹ đạo dao động là: L = 2 A = 10 cm
Tốc độ cực đại là v max = 10 π cm/s
Gia tốc cực đại là a max = ω 2 A = 20 π 2 c m / s 2
Tốc độ trung bình trong một chu kì là v t b = s T = 4 A T = 4.5 1 = 20 cm/s.
Tại t = 0 thì x = 5 ® vật ở vị trí biên.
® Các phát biểu đúng là: c, e.
Đáp án C

Chọn đáp án D
Tốc độ bằng một nửa tốc độ cực dại có li độ tương ứng: x = 3 2 A
→ Thời gian ngắn nhất vật đi từ x = 0 đến x = 3 2 A là: Δ t = T 6

tại \(t=0\) vật tại \(x=5\sqrt{3}\)
\(v>0\)
\Rightarrow \(s=4A+17-5\sqrt{3}\)
sử dung công thức
\(s=2A.\sin\left(\frac{\omega.t1}{2}\right)\)
\Rightarrow t1 = ?
vậy khoảng thời gian nhỏ nhất là \(t=T+t1\)
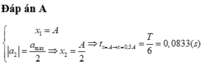


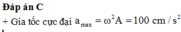
Chu kì: T = 0,5s
Độ lớn của gia tốc: \(|a| = \omega^2|x|\) nên khi khi \(|a| = \frac{a_{max}}{2}\) thì \(x = \pm\frac{A}{2}\)
Biểu diễn bằng véc tơ quay ta có:
M N x 60 0
Ban đầu véc tơ quay xuất phát tại M, thời điểm gần nhất thỏa mãn điều kiện, véc tơ quay đến N, góc quay 600
Thời gian: \(t = \frac{60}{360}T = \frac{T}{6}\)=0,5/6 = 0,083s
c