Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D
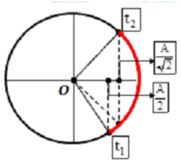
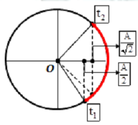
t 1 = π 15 s → W d W = 3 4 ⇒ x 1 = ± A 2 t 2 = 11 π 60 s → W d = W t ⇒ x 2 = ± A 2
T 6 + T 8 ⏟ t 2 − t 1 = 11 π 60 − π 15 ⇒ T = 2 π 5
⇒ ω = 5 r a d / s
W = 1 2 m ω 2 A 2
⇒ A = 2 W m ω 2 = 0 , 08 m = 8 c m .
Chú ý: T là chu kì của li độ, cơ năng của vật W = 10.4 = 40mJ.

Đáp án D
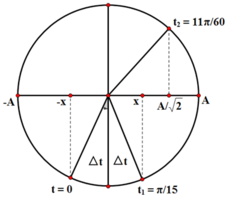
Ta biểu diễn đồ thị trên vòng tròn lượng giác trục của li độ
Tại thời điểm ban đầu, động năng tăng dần đến cực đại nên vật đang tiến dần đến VTCB.
Tại thời điểm 1/15 (s) vật vừa đi qua VTCB và có động năng như ban đầu nên 2 thời điểm li độ đối xứng qua VTCB.
Tại thời điểm 11/60 (s) động năng bằng thế năng lần thứ 2 tại vị trí A2.
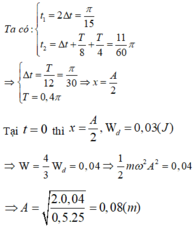
Suy ra độ dài quỹ đạo của vật là: S = 2A= 8.2= 16

Hướng dẫn:
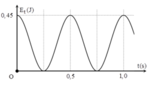
+ Từ đồ thị ta thấy rằng thế năng biến thiên với chu kì 0,5 s vậy chu kì của dao động là T = 1 s → ω = 2π rad/s.
Biên độ của dao động được xác định bởi E = 1 2 m ω 2 A 2 → A = 2 E m ω 2 = 2.0 , 45 1. 2 π 2 = 15 cm.
Đáp án C

Giải thích: Đáp án C
+ Chu kì biến thiên của động năng là 0,5 s → T = 1 s → w = 2p rad s
Trạng thái M ứng với 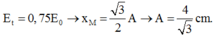
+ Trạng thái N ứng với 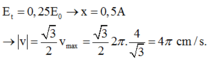

Giải thích: Đáp án C
Phương pháp: Định luật bảo toàn năng lượng
Cách giải:
Ta thấy động năng của vật bằng thế năng ứng với các vị trí li độ lần lượt là
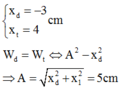

dùng công thức giải nhanh
Wđ=nWt => x=\(\pm\frac{A}{\sqrt{n+1}}\)
Ta có Wđ=3Wt =>2= \(\frac{A}{\sqrt{3+1}}=\frac{A}{2}\)
=>A=4
Vậy ta có biên độ dao động là 4cm
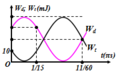
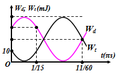

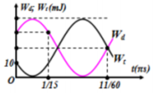
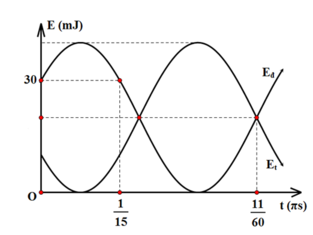


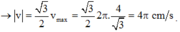
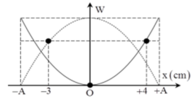

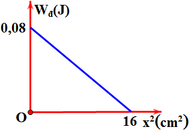
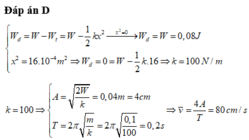
Chú ý: T là chu kì của li độ, cơ năng của vật W = 10.4 = 40mJ