Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử pt dao động của vật có dạng:
\(x=Acos\left(5t+\varphi\right)\left(cm\right)\)
\(\Rightarrow v=-5Asin\left(5t+\varphi\right)=5Acos\left(\dfrac{\pi}{2}+5t+\varphi\right)\left(\text{cm/s}\right)\)
Tại \(t=0:\)\(\left\{{}\begin{matrix}x=-2\left(cm\right)\\v=10\left(\text{cm/s}\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_0=Acos\varphi=-2\left(cm\right)\\v_0=5Acos\left(\dfrac{\pi}{2}+\varphi\right)=10\left(\text{cm/s}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cos\varphi=-\dfrac{2}{A}\left(1\right)\\5A\left(cos\dfrac{\pi}{2}.cos\varphi-sin\dfrac{\pi}{2}.sin\varphi\right)=10\end{matrix}\right.\)
\(\Rightarrow5A.\left(-sin\varphi\right)=10\Leftrightarrow sin\varphi=\dfrac{-2}{A}\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow\varphi=\dfrac{-3\pi}{4}\left(rad\right);A=2\sqrt{2}\left(cm\right)\)
Vậy ta có ptdđ của vật: \(x=2\sqrt{2}cos\left(5t-\dfrac{3\pi}{4}\right)\left(cm\right)\)
b)\(v_{max}=\omega A=5A=10\sqrt{2}\left(\text{cm/s}\right)\)
\(a_{max}=\omega^2A=50\sqrt{2}\left(\text{cm/s}^2\right)\)
c) \(\alpha=\Delta t.\omega=1,4\pi.5=7\pi\left(rad\right)=6\pi+\pi\left(rad\right)\)
\(\Rightarrow S=3.4A+2\sqrt{2}-2+2\sqrt{2}+2=12A+4\sqrt{2}=28\sqrt{2}\left(cm\right)\)

1. Vật tại vị trí cân bằng có vmax = ωA = 20 cm/s
Khi vật có tốc độ bằng v = \(\omega.\sqrt{A^2-x^2}=10\left(\dfrac{cm}{s}\right)\)
Gia tốc của vật có độ lớn a = ω2x = \(40\sqrt{3}\) cm/s2
Từ đó A = 5 cm, ω = 4rad/s
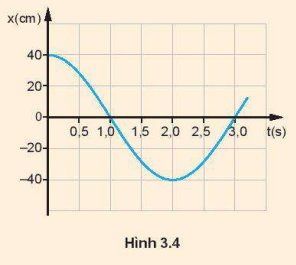
2. Từ đồ thị ta thấy:
Biên độ A = 40 cm, chu kì T = 4s
a) Tốc độ của vật ở thời điểm t = 0s bằng v = 0 (cm/s) vì ở vị trí biên.
b) Tốc độ cực đại của vật là vmax = ωA = 20π (rad/s).
c) Gia tốc của vật tại thời điểm t = 1,0 s là a= ω2A=10π2 (rad/s) đạt giá trị lớn nhất vì tại vị trí cân bằng.

\(f=5Hz=>\omega=\dfrac{2\pi}{f}=\dfrac{2\pi}{5}
\\
A^2=x^2+\dfrac{v^2}{\omega^2}\\
< =>v^2=\omega^2\left(A^2-x^2\right)\\
< =>v^2=\dfrac{2\pi}{5}\left(4^2-2^2\right)\\
< =>v^2=\dfrac{24\pi}{5}\\
< =>v=\dfrac{2\sqrt{6}\pi}{5}\)
\(a=A\omega^2\\
< =>a=4.\left(\dfrac{2\pi}{5}\right)^2\\
< =>a=\dfrac{16\pi}{25}\)

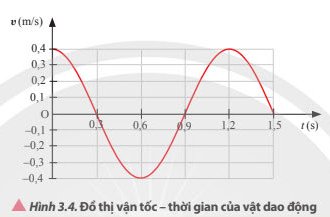
Tốc độ cực đại của vật trong quá trình dao động là 0,4 m/s
Thế năng cực đại của vật trong quá trình dao động là
\(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}.2.0,4^2=0,16\left(J\right)\).

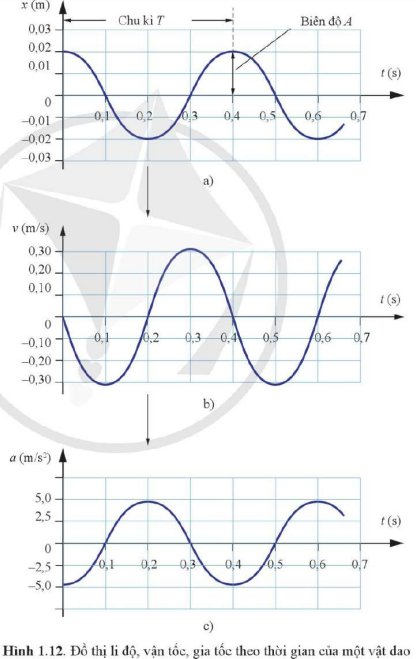
`***` Hình `a`:
`a, \omega =[2\pi]/[0,4]=5\pi (rad//s)`
`b, A=0,03(m)=3(cm)`
`c, v_[max]=5\pi .3=15 \pi(cm//s)`
`d, a_[max]=(5\pi)^2 .3=75 \pi^2 (cm//s^2)`
`***` Hình `b`:
`a, \omega =[2\pi]/[0,4]= 5 \pi(rad//s)`
`b, A=[0,3]/[5\pi]=3/[50 \pi] (m)=6/[\pi] (cm)`
`c, v_[max]=30 (cm//s)`
`d, a_[max]=30.5\pi=150\pi (cm//s^2)`
`***` Hình `c`:
`a, \omega=[2\pi]/[0,4]=5\pi (rad//s)`
`b, A=5/[(5\pi)^2]=1/[5\pi^2] (m)`
`c, v_[max]=5\pi . 1/[5\pi^2]=1/[\pi] (m//s)`
`d, a_[max]=5(m//s^2)`
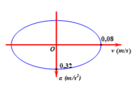
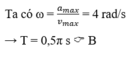

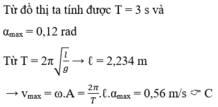

Vì tốc độ trễ pha hơn gia tốc `\pi/2` nên ta có đường tròn lượng giác như sau:
Từ ĐTLG `=>` Khi tốc độ của vật bằng `[v_[max]]/2` thì gia tốc có độ lớn là `\sqrt{3}/2 a_[max]`.