Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp: Sử dụng đường tròn lượng giác
Ta có T = 0,4s => t = 11T + T/4
Ta thấy vật sẽ đi được 11 chu kì và trở về vị trí cũ rồi thực hiện được ¼ chu kì nữa như hình vẽ:
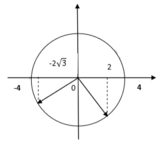
Quãng đường vật đi được sau khoảng thời gian t = 4,5s là:
![]()

Nghĩa là nó sẽ đi một lần A/2, 1 lần A, và 1 lần A/3
\(\Rightarrow\varphi=\dfrac{\pi}{3}+\dfrac{\pi}{2}+\dfrac{\pi}{2}-arc\cos\left(\dfrac{1}{3}\right)=...\left(rad\right)\)
\(\Rightarrow t=\dfrac{\varphi}{\omega}=\dfrac{\varphi}{3\pi}\left(s\right)\)

\(20-10\sqrt{2\left(A-\frac{A}{\sqrt{2}}\right)}\Rightarrow\frac{T}{4}=1\Rightarrow T=4\left(s\right)\)
\(S=S_{2012}-S_{2011}=A\sqrt{2}=10\sqrt{2}\) (cm)
Không có đáp án đó nhưng bạn giải thích cách làm của bạn cho mình với.

Để tính quãng đường vật đi được sau 0,25 s, ta có thể sử dụng phương trình dao động điều hòa x = A * cos(2π/T * t + φ), trong đó x là vị trí của vật (cm), A là biên độ của vật (cm), T là chu kỳ của dao động (s), t là thời gian (s), và φ là góc pha ban đầu (rad).
Trong trường hợp này, phương trình dao động là x = 4cos(4πt + π/4). Ta có thể nhận thấy rằng biên độ của vật là 4 cm và chu kỳ của dao động là T = 1/4 s.
Để tính quãng đường vật đi được sau 0,25 s, ta thay t = 0,25 vào phương trình:
x = 4cos(4π * 0,25 + π/4)
x = 4cos(π + π/4)
x = 4cos(5π/4)
x ≈ 4 * (-0,7071)
x ≈ -2,8284 cm
Vậy, quãng đường vật đi được sau 0,25 s kể từ khi bắt đầu chuyển động là khoảng -2,8284 cm.

Trong giây thứ 2019 thiệt à?
Vậy thì khó gì, vẽ đường tròn ra và phân tích thôi
\(T=\dfrac{2\pi}{\pi}=2\left(s\right)\) => 1s nó đi được 4+4=8 (cm)
Trong khoảng thời gian từ t=0 đến t=2018 thì vật đi được 2018/2=1009 chu kỳ và trở lại vị trí ban đầu=> Đi được 8(cm)
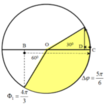
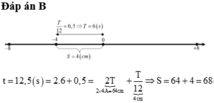

Chu kì: \(T=2\pi/\omega=0,4s\)
Ta có: \(t=2s=5.T\)
Trong mỗi chu kì, quãng đường đi được là 4A
Vậy trong 5 chu kì quãng đường đi được là: \(5.4A=20A=20.4=80(cm)\)
cho em hỏi là 5T đó ở đâu ạ