Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x=Acos(\(\omega t+\varphi\))
Tại thời điểm t=0, ta có:
\(\frac{A}{2}=Acos\left(\varphi\right)\) \(\Rightarrow\)\(\varphi=-\frac{\pi}{6}\)(do vật chuyển động theo chiều dương)
\(\Rightarrow\) \(x=Acos\left(\omega t-\frac{\pi}{6}\right)\)
cái này mình tưởng phải bằng: x=Acos(\(\omega t+\frac{\pi}{3}\)) chứ.

Biên độ: \(A^2=x^2+\dfrac{v^2}{\omega^2}=(2\sqrt 3)^2+\dfrac{(20\sqrt 2)^2}{(10\sqrt 2)^2}\)
\(\Rightarrow A = 4cm\)
\(\cos\varphi = \dfrac{x}{A}=\dfrac{2\sqrt 3}{4}\)
\(v>0\Rightarrow \varphi < 0\)
Suy ra: \(\varphi=-\dfrac{\pi}{6}(rad)\)
Vậy: \(x=4\cos(10\sqrt 2 t-\dfrac{\pi}{6})(cm)\)

Đáp án D
Chu kì dao động
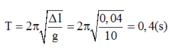
Trong một chu kì dao động, thời gian lò xo bị nén là khoảng thời gian vật đi từ x = ∆l đến x = A rồi trở về x = ∆l, tức là ∆t = 2t0 với t0 là thời gian đi từ x = ∆l đến x = A (giả sử chiều dương của trục tọa độ hướng lên).
Theo giả thiết:
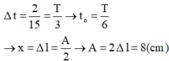
Khi lò xo giãn 8 cm ![]() vật đang chuyển động chậm dần đều nên đang đi ra biên, đi theo chiều dương hướng xuống
vật đang chuyển động chậm dần đều nên đang đi ra biên, đi theo chiều dương hướng xuống
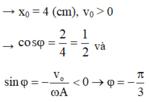

 \
\
