Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
+ Để vật dao động với cơ năng cực đại khi Amax.
+ x = x1 + x2 => x1 = x – x2 = A cos(ωt – π/3) - A2 cos(ωt – π/2)
= A cos(ωt – π/3) + A2 cos(ωt + π/2)
+ A12 =102 = A2 + A22 + 2AA2cos(- π/3 - π/2).
ó A22 - AA2√3-100 + A2 = 0 (1).
+ Để phương trình (1) có nghiệm đối với A2 <=> Δ = (-A√3)2 – 4.1.(-100 + A2) ≥ 0
=> 0 ≤ A ≤ 20 cm.
=> Amax = 20 thay vào (1) tìm được A2 = 10√3 cm.

Đáp án A
Vị trí có li độ x = 2 2 A vật có E d = E t = 0 , 5 E = 0 , 25 m ω 2 A 2 .

Đáp án A
Phương pháp: Áp dụng định luật bảo toàn cơ năng W = Wđ + Wt
Cách giải:
Ta có : 
Khi 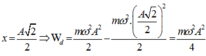

Phương pháp: Công thức tính thế năng, động năng và cơ năng:
Định luật bảo toàn cơ năng: W = Wđ + Wt
Cách giải:
+ Hai vật dao động cùng khối lượng gắn vào hai lò xo dao động cùng tần số và ngược pha nhau => Phương trình của li độ và vận tốc của hai dao động là:
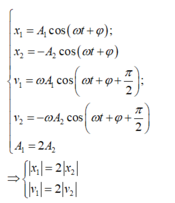
Công thức tính động năng và cơ năng :
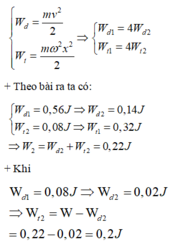
Đáp án A

Năng lượng dao động bằng động năng hoặc cơ năng cực đại:
\(W=\dfrac{1}{2}m.v_{max}^2=\dfrac{1}{2}m.\omega^2.A^2=0,5.0,5.(10\pi)^2.0,02^2=0,01J\)

Chọn đáp án D
@ Lời giải:
+ Thế năng của vật dao động điều hòa biến thiên tuần hoàn với tần số góc:
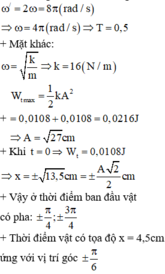
+ Vậy thời điểm vật qua vị trí x = 4,5cm lần đầu tiên là: T 24 = 1 48 s

Do thời gian biến thiên vận tốc là T/4, nếu biểu diễn vận tốc bằng véc tơ quay thì góc quay là 900 nên ta có:
\((\dfrac{-20\pi\sqrt 3}{v_0})^2+(\dfrac{-20\pi}{v_0})^2=1\)
\(\Rightarrow v_0=40\pi(cm/s)\)
\(\Rightarrow \omega = \dfrac{40\pi}{10}=4\pi(rad/s)\)
\(\Rightarrow f = 2Hz\)
Chọn B.
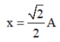

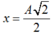
\(x=A.\cos^2(\omega t+\dfrac{\pi}{3})\) không phải dao động điều hoà bạn nhé.
Đó chỉ là dao động tuần hoàn mà thôi.
Sao là vậy bạn?