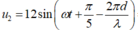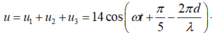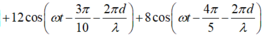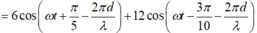Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Hướng dẫn: Chọn đáp án B
Kinh nghiệm: Bài toán cho x1 và xu hướng đang tăng (v1 > 0) hoặc đang giảm (v1 <0) thì nên làm theo cách 2.
Cách 1: Viết lại phương trình li độ vận tốc:
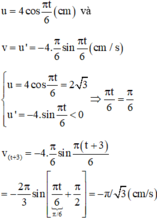
Cách 2: Chọn trạng thái tại thời điểm t1 là trạng thái ban đầu Þj= p/6 Pha dao động ở thời điểm tiếp theo:
\(\lambda = v/f = 80/20 = 4cm.\)
\(\triangle \varphi = \pi-0=\pi.\)
Nhận xét: \(BM-AM=(BI+IM)-(AI-IM)=2MI\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{BM-AM}{\lambda}-\frac{\triangle\varphi}{2\pi})|\\=|2a\cos\pi(\frac{2MI}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{6}{4}-\frac{\pi}{2\pi})| = |-2a|=2a=10 mm.\)
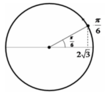
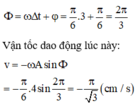
Chọn đáp án A
f = ω 2 π = 25 H z ⇒ λ = v f = 75 25 = 3 c m
Hai nguồn dao động ngược pha → điều kiện để điểm M dao động cực đại là ∆ d = ( 2 k + 1 ) λ 2
→ -12 ≤ (2k + 1).1,5 ≤ 12 → -4,5 ≤ k ≤ 3,5 → k = -4,...0,...3 → trong khoảng AB có 8 điểm dao động với biên độ cực đại.
Mỗi đường cực đại cắt đường tròn đường kính AB tại hai điểm nên số điểm dao động có biên độ cực đại trên đường tròn đường kính AB là 16
Đáp án B
f = ω 2 π = 25 ( H z ) ⇒ λ = v f = 75 25 = 3 ( c m )
Hai nguồn dao động ngược pha → điều kiện để điểm M dao động cực đại là ∆ d = ( 2 k + 1 ) λ 2
→ –12 ≤ (2k + 1).1,5 ≤ 12 → –4,5 ≤ k ≤ 3,5 → k = –4,...0,...3 → trong khoảng AB có 8 điểm dao động với biên độ cực đại. A –
Mỗi đường cực đại cắt đường tròn đường kính AB tại hai điểm nên số điểm dao động có biên độ cực đại trên đường tròn đường kính AB là 16.
