Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mỗi câu hỏi bạn nên hỏi 1 bài thôi nhé.
Bài 1:
Áp dụng công thức độc lập thời gian: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow A^2= 2^2+\dfrac{(4\pi\sqrt 3)^2}{\omega^2}=3^2+\dfrac{(2\pi\sqrt 7)^2}{\omega^2}\)
\(\Rightarrow \omega=2\pi\) (rad/s)
Và \(A=4\) (cm)
Tìm pha ban đầu \(\varphi\) bằng cách: \(\cos(\varphi)=\dfrac{x_1}{A}=\dfrac{1}{2}\)
Ban đầu vật đi theo chiều dương \(\rightarrow \varphi <0\)
\(\Rightarrow \varphi=-\dfrac{\pi}{3}\)
Vậy PT: \(x=4\cos(2\pi t-\dfrac{\pi}{3})\) (cm)
b)
M N 4 -4 -2 O
Biểu diễn dao động của vật bằng véc tơ quay như hình vẽ
Thời điểm đầu tiên vật qua x1 theo chiều âm ứng với véc tơ quay từ M đến N
Góc quay \(\alpha =60.2=120^0\)
Thời gian: \(i=\dfrac{120}{360}T=\dfrac{1}{3}s\)
Bài 2:
O chính là vị trí cân bằng với 2 biên là M, N
Thời gian vật đi từ O đến M là T/4
\(\Rightarrow T/4=6\Rightarrow T =24s\)
Biểu diễn dao động điều hoà bằng véc tơ quay ta có:
M N O P Q I
Vật đi từ O đến trung điểm I của ON ứng với véc tơ quay từ P đến Q
Góc quay: \(\alpha =30^0\)
Thời gian: \(t=\dfrac{30}{360}T=\dfrac{1}{12}.24=2(s)\)

Chọn đáp án C
+ Theo đề: x = x 1 − x 2 = 10 3 cos 4 π t + φ c m
+ Giả sử chọn t = 0 ⇒ x = x 0 = 10 3 c m nghĩa là t 1 : x = 10 3 cos 4 π t 1 = ± 15 ⇔ cos 4 π t 1 = ± 3 2
Tại t 1 : x = 10 3 cos 4 π t 1 = ± 15 ⇔ cos 4 π t 1 = ± 3 2
⇒ 4 π t 1 = π 6 ⇒ t 1 = 1 24 s (Từ biên A đến vị trí A 3 2 )
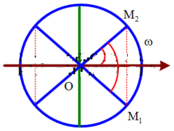
+ Theo hình vẽ ở tai thời điểm t1: 4 π t 1 = π 6 ⇒ t 1 = 1 24 s
Theo hình vẽ dễ thấy 2 thời điểm gần nhất là 2 lần t1
Từ M1 đến M2: t 2 − t 1 = 2 t 1 = 2 24 = 1 12 s t

Chọn đáp án C
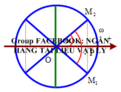
Theo đề: x = x 1 − x 2 = 10 3 cos 4 π t + φ c m
Giả sử chọn φ = 0 nghĩa là t = 0 ⇒ x = x 0 = 10 3 c m
Tại t 1 : x = 10 3 cos 4 π t 1 = ± 15 ⇔ cos 4 π t 1 = ± 3 2
⇒ 4 π t 1 = π 6 ⇒ t 1 = 1 24 s (Từ biên A đến vị trí A 3 2 )
Theo hình vẽ ở tai thời điểm t 1 : 4 π t 1 = π 6 ⇒ t 1 = 1 24 s
Theo hình vẽ dễ thấy 2 thời điểm gần nhất là 2 lần t 1
Từ M 1 đ ế n M 2 : t 2 − t 1 = 2 t 1 = 2 24 = 1 12 s t

Tần số góc của dao động
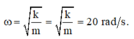
+ Vận tóc cực đại cực đại của dao động
![]()
+ Biểu diễn dao động của vật tương ứng trên đường tròn.
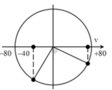
→ Khoảng thời gian tương ứng
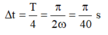
Đáp án D

• Ta có ω = k m = 20 r a d / s → v m a x = ω A = 80 c m / s rad/s
• Khoảng thời gian ngắn nhất để vận tốc biến đổi từ - 40 = - v m a x 2 đến 40 3 = v m a x 3 2 theo trục phân bố thời gian là T 40 = π 40 s. Chọn B.

Chọn A
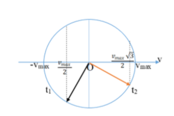
+ Thay k = 100N/m và m = 250g = 0,25kg vào
ω = k m => ω = 20 rad/s => T = π/10 (s).
+ vmax = ωA = 20.4 = 80 cm/s.
+ v1 = -40 cm/s = - vmax/2;
v2 = 40 3 cm/s = vmax 3 /2.
+ Sử dụng vòng tròn: tmin = T 12 + T 6 = T 4 = π 40 s.

Đáp án B
+ Khoảng cách giữa hai dao động được biểu diễn bằng một hàm điều hòa
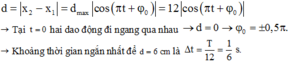

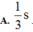
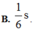
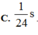
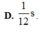
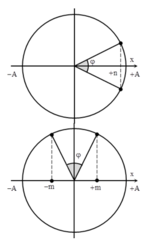

Theo đề bài thì MN là quỹ đạo của dao động, do đó biên độ \(A=MN/2=12/2=6cm\)
Thời gian vật đi từ M đến N là nửa chu kì, do vậy \(T=2.0,314=0,2\pi(s)\)
\(\Rightarrow \omega=\dfrac{2\pi}{T}=10(rad/s)\)
Khi vật cách M 4 cm thì nó cách trung điểm M là 2 cm (là vị trí cân bằng) dó vậy, li độ dao động là \(x=2cm\)
Áp dụng công thức độc lập: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow v = \omega.\sqrt{A^2-x^2}=10.\sqrt{6^2-2^2}10\sqrt {34}(cm/s)\)
cảm ơn ạ