Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1)
O 8 -8 4 M N P x
Pha ban đầu bằng 0 nên véc tơ quay xuất phát tại M.
Khi vật qua x = 4 cm thì véc tơ quay quay đến N hoặc P.
Cho véc tơ quay xuất phát ở M quay ngược chiều kim đồng hồ. Khi nó quay được 1004 vòng thì nó qua N và P là 2008 lần, lần cuối cùng nó quay từ M đến N.
Vậy thời gian tương ứng: \(t=1004T+\dfrac{60}{360}T=(1004+\dfrac{1}{6}).\dfrac{2\pi}{10\pi}=200,83(s) \)

+ Tại t = 0 vật đang ở vị trí biên dương.
Trong một chu kì vật đi qua vị trí x = 5 cm hai lần → ta tách 2008 = 2006 + 2.
+ Tổng thời gian thoãn mãn yêu cầu bài toán là:
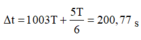
Đáp án A

Chọn C
+ Chu kỳ dao động T = 0,2 (s)
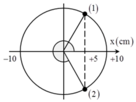
+ t = 0: x=10 cos0 = 10cm = +A.
+ Thời gian vật đi từ vị trí ban đầu x = +A tới x = 5cm = A/2 chuyển động theo chiều dương lần thứ nhất là:
t1 = tA→-A + t-A→O + tO→A/2
![]()
+ Còn 2008 lần sau đó, cứ một chu kì vật lại qua x = A/2 theo chiều dương một lần nên cần thời gian 2008T.
+ Thời điểm vật đi qua vị trí li độ x = 5cm lần thứ 2009 theo chiều dương:
t = t1 + 2008T = 401,76 s.

Chọn B
+ Chu kỳ dao động T = 0,2 (s)
+ t = 0: x=10 cos0 = 10cm = +A.
+ Trong một chu kì vật đi qua vị trí x = A/2 hai lần nên 2006 lần cần thời gian 1003T.
+ Thời gian 2 lần còn lại vật đi từ vị trí ban đầu x = +A tới x = 5cm = A/2 là:
t1 = tA→-A + t-A→O + tO→A/2
=![]()
+ Thời điểm vật đi qua vị trí N có li độ xN = 5cm lần thứ 2008 là:
t = t1 + 1003T ≈ 200,8 (s).

Đáp án B
Phương pháp: Sử dụng đường tròn để tính thời gian trong dao động điều hòa
Cách giải:
PT dao động x = 10cos(10πt) cm => chu kì dao động T = 0,2s
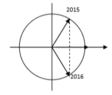
Khoảng thời gian vật đi từ vị trí x = 5cm lần thứ 2015 đến lần thứ 2016 là: Δt = T/2 + T/6 = 2/15s
=> Chọn B

Ta có:
- Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{4\pi}=0,5s\)
\(\Delta t=t_1-t_2=\dfrac{7}{48}s\)
Góc vật quét được khi từ thời điểm \(t_1\) đến \(t_2\) : \(\Delta\varphi=\omega\Delta t=4\pi.\dfrac{7}{48}=105^o\)
Tại thời điểm \(t_1\) vật đang có li độ: \(x=5\left(cm\right)=\dfrac{A}{2}\)
+ Với \(t_1\left(1\right)\) ta có, li độ của vật tại thời điểm \(t_1\left(2\right)\)
\(x_1=A.sin\left(15^o\right)=2,59cm\)
+ Với \(t_2\left(1\right)\) ta có, li độ của vật tại thời điểm \(t_2\left(2\right)\)
\(x_2=A.cos\left(15^o\right)=9,66\left(cm\right)\)\(\Rightarrow A\)

a/w=2pi/T
L=2A suy ra x=5cos(pi.t+pi/3); v=-5pi sin (pi.t+pi/3); a=-5pi2 cos(pi.t+pi/3)
b/x=-5 đến x=5 là t=T/2=1s ;x=0 đến x=5 là t=T/4=0,5s
C/thế t=3s vào pt x suy ra x=-5/2 suy ra pha là\(\pm\)2pi/3
d/thế t=2,5s vào pt vận tốc và gia tốc
e/x2 +\(\dfrac{v^2}{w^2}\) =A2 ;a=-w2 x

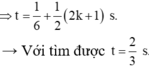

\(\alpha =\omega .t=2\pi .\frac{28}{3}=\frac{56\pi }{3}=18\pi +\frac{2\pi }{3}=9.2\pi +\frac{2\pi }{3}\)
+) TH1: nếu thời điểm t , x=-5cm vật ở nửa trên đường tròn =>sau khi quét góc \(9.2\pi +\frac{2\pi }{3}\)vật sẽ đến điểm x=-5 nhưng ở nửa dưới đg tròn
+)TH2: nếu thời điểm t , x=-5cm vật ở nửa dưới đg trong =>sau khi quét góc \(9.2\pi +\frac{2\pi }{3}\)vật sẽ đến vị trí biên dương x=10cm
=>chọn C