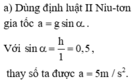Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TH1: Co ma sat
\(F-mg\sin30^0-\mu mg=0\Leftrightarrow F=1.10.\dfrac{1}{2}+0,1.1.10=6\left(N\right)\)
\(\Rightarrow A_F=F.s=6.0,2=1,2\left(J\right)\)
\(A_{ms}=F_{ms}.s=0,1.1.10.0,2=0,2\left(J\right)\)
\(A_P=mg\sin30^0.s=1.10.\dfrac{1}{2}.0,2=1\left(J\right)\)
TH2: Khong co ma sat
\(F=mg\sin30^0=\dfrac{10}{2}=5\left(N\right)\)
\(\Rightarrow A_F=F.s=5.0,2=1\left(J\right)=A_P\)
Các công này tính theo độ lớn, ko phải theo giá trị nên nó luôn dương

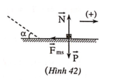
góc tạo bởi mặt phẳng nghiêng và phương ngang
sin\(\alpha=\dfrac{h}{l}\Rightarrow\alpha=30^0\)
\(\overrightarrow{P}+\overrightarrow{N}=m.\overrightarrow{a}\)
chiếu lên trục Ox phương song song mặt phẳng nghiêng, chiều dương cùng chiều chuyển động
sin\(\alpha\).P=m.a\(\Rightarrow\)a=5m/s2
thời gian vật đi hết dốc t=\(\sqrt{\dfrac{l}{2a}}\)=2s
b) khi đi hết dốc vận tốc của vật là v=v0+a.t=10m/s2
khi xuống dốc xuất hiện ma sát
\(\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m.\overrightarrow{a'}\)
chiếu lên trục Ox phương nằm ngang chiều dương cùng chiều chuyển động
-Fms=m.a' (1)
chiếu lên trục Oy phương thẳng đứng chiều dương hướng lên trên
N=P=m.g (2)
từ (1),(2)\(\Rightarrow\)a'=-5m/s2
thời gian vật chuyển động trên mặt phẳng đến khi dừng lại là (v1=0)
t=\(\dfrac{v_1-v}{a'}=2s\)


200g=0,2kg
các lực tác dụng lên vật khi ở trên mặt phẳng nghiêng
\(\overrightarrow{P}+\overrightarrow{N}=m.\overrightarrow{a}\)
chiếu lên trục Ox có phương song song với mặt phẳng nghiêng, chiều dương cùng chiều chuyển động
P.sin\(\alpha\)=m.a\(\Rightarrow\)a=5m/s2
vận tốc vật khi xuống tới chân dốc
v2-v02=2as\(\Rightarrow\)v=\(4\sqrt{5}\)m/s
khi xuống chân dốc trượt trên mặt phẳng ngang xuất hiện ma sát
các lực tác dụng lên vật lúc này
\(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=m.\overrightarrow{a'}\)
chiếu lên trục Ox có phương nằm ngang chiều dương cùng chiều chuyển động của vật
-Fms=m.a'\(\Rightarrow-\mu.N=m.a'\) (1)
chiếu lên trục Oy có phương thẳng đứng chiều dương hướng lên trên
N=P=m.g (2)
từ (1),(2)\(\Rightarrow\)a'=-2m/s2
thời gian vật chuyển động trên mặt phẳng đến khi dừng lại là (v1=0)
t=\(\dfrac{v_1-v}{a'}\)=\(2\sqrt{5}s\)

M N P H 10m 30 P S
Chọn mốc thế năng tại chân mặt phẳng nghiêng
\(MN=\dfrac{10}{\sin 30^0}=20m\)
Lực ma sát trên mặt phẳng nghiêng: \(F_{ms1}=\mu mg\cos 30^0=0,1.mg.\dfrac{\sqrt 3}{2}\)
Lực ma sát trên mặt phẳng ngang: \(F_{ms2}=\mu.mg=0,1.mg\)
Cơ năng ban đầu: \(W=m.g.h=10.mg\)
Công của lực ma sát trong cả quá trình: \(A_{ms}=F_{ms1}.MN+F_{ms2}.NP=0,1.mg.\dfrac{\sqrt 3}{2}.20+0,1mg.S\)
Vật dừng lại khi cơ năng bằng 0.
Áp dụng độ giảm cơ năng bằng công của lực ma sát ta có:
\(W-0=A_{ms}\)
\(\Rightarrow 10.mg =0,1.mg.\dfrac{\sqrt 3}{2}.20+0,1mg.S\)
\(\Rightarrow 10 =\sqrt 3+0,1.S\Rightarrow S=82,68(m)\)
Tìm vBvB
Vật chuyển động trên mặt phẳng nghiêng :
P→P→ + N→N→ + f→msf→ms = ma→ma→ (11)
ch(11) / Oy : −Pcosα+N=0−Pcosα+N=0
⇒fms=μPcosα⇒fms=μPcosα
ch(11) /Ox : Psinα−fms=maPsinα−fms=ma
aa = Psinα−μPcosαmPsinα−μPcosαm
=(sinα−μcosα)g=3,43(m/s2).=(sinα−μcosα)g=3,43(m/s2).
vBvB = 2al−−−√2al ≈8,3≈8,3 (m).
b) Tìm tt.
Vật chuyển động trên mặt ngang :
P→P→ + N→1N→1 + f′→