Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D
Vật rời khỏi giá đỡ khi phản lực N = 0
Áp dụng định luật II Newton cho vật trên ván chuyển động có gia tốc a, ta được:
mg – N – Fđh = ma
Vật rời ván khi N = 0→Fđh = k.∆l = m(g-a)→∆l = 9cm
Ban đầu ván ở vị trí lò xo giãn 1cm nên khi vật rời ván, ván đi được:
S = ∆l – 1 = 8cm
Khi đó tốc độ của vật 
vật cách VTCB là 1cm (chiều dương hướng xuống → x = 1cm)
=>Biên độ dao động của vật:
Giải thích: Đáp án A
Phương pháp:
- Áp dụng công thức tính vận tốc và quãng đường của vật trong chuyển động thẳng nhanh dần đều
- Áp dụng định luật II Niuton
Cách giải:
- Tần số góc: 
- Vật chuyển động nhanh dần đều cùng ván, khi bắt đầu rời khỏi tấm ván, vận tốc và quãng đường vật đi
được lúc đó là: 
- Khi vật rời ván, áp lực do vật tác dụng lên ván bằng 0 nên chỉ còn lực đàn hồi và trọng lực tác dụng lên tấm ván.
ADĐL II Niuton ta được: 
Đáp án C
Giá ban đầu giữ cho lò xo không biến dạng sau đó giá bắt đầu chuyển động nhanh dần đều với gia tốc a.
Khi bắt đầu rời giá đỡ, vật đã đi được quãng đường S và gia tốc cũng là a:
Thời gian tính đến lúc rời giá đỡ là:
Tốc độ và độ lớn li độ của vật lúc rời giá đỡ là:
Biên độ dao động:
Chọn đáp ánC
Giá ban đầu giữ cho lò xo không biến dạng sau đó giá bắt đầu chuyển động nhanh dần đều với gia tốc a. Khi bắt đầu rời giá đỡ, vật đã đi được quãng đường S và gia tốc cũng là a:
a = m g − k S m ⇒ m ( g − a ) k = 0 , 08 m
Thời gian tính đến lúc rời giá đỡ là:
S = a t 2 2 ⇒ t = 2 S a = 0 , 2 2 ( s )
Tốc độ và độ lớn li độ của vật lúc rời giá đỡ là:
v = a t = 0 , 4 2 ( m / s ) x 1 = S − Δ l 0 = S − m g k = 0 , 02 m
Biên độ dao động:
A = x 1 2 + v 1 2 ω 2 = x 1 2 + v 1 2 m k = 0 , 02 2 + 0 , 16.2.1 100 = 0 , 06 m
Chọn chiều dương hướng xuống
Ban đầu, tại vị trí cân bẳng O1, lò xo dãn một đoạn: ∆ l = m g k = 5 c m
Giá đỡ M chuyển động nhanh dần đều hướng xuống ⇒ lực quán tính F hướng lên ⇒ vị trí cân bằng khi có giá đỡ M là O2, với
Giá đỡ đi xuống đến vị trí O2, vật và giá đỡ sẽ cách nhau
⇒ Suy ra vật và giá đỡ có tốc độ:
Khi tách ra, vị trí cân bằng của vật là O1 ⇒ vật có li độ: x = - 1 cm
Thời gian vật đi từ x = - 1 cm → x = A = 3 cm (lo xo có chiều dài lớn nhất lần đầu tiên) là
t = 0,1351 s
Tính từ O2, giá đỡ M đi được quãng đường:
s = v t + 1 2 a t 2 = 0 , 0723 m = 7 , 23 c m
Suy ra, khoảng cách 2 vật là: d = 7,23 - (1 + 3)= 3,23 cm ⇒ gần 3 cm nhất
Đáp án D
Đáp án B
Hướng dẫn:
Nhận thấy rằng trong quá trình chuyển động của giá đỡ M, sẽ có thời điểm M tách khỏi m. Khi đó M tiếp tục chuyển động với gia tốc a, vật m sẽ dao động điều hòa quanh vị trí cân bằng của nó.
+ Tại vị trí cân bằng O của m, lò xo giãn một đoạn Δ l 0 = m g k = 0 , 1.10 20 = 5 cm.
Tần số góc của dao động ω = k m = 20 0 , 1 = 10 2 rad/s → T ≈
+ Ta xác định xem, tại vị trí hai vật tách khỏi nhau vật m có li độ và vận tốc như thé nào.
Phương trình động lực học cho vật m: P – N – Fdh = ma → tại vị trí vật m rời khỏi giá đỡ thì N = 0
→ Vậy độ giãn của lò xo khi đó là Δ l = m g − m a k = 0 , 1.10 − 0 , 1.2 20 = 4 cm.
→ Vận tốc của vật m ngay khi rời giá đỡ được xác định dựa vào công thức liên hệ giữa vận tốc, gia tốc và quãng đường trong chuyển động biến đổi đều: v = 2 a s = 2.2.0 , 02 = 0 , 4 m/s.
→ Biên độ dao động của vật m là: A ' = x ' 2 + v ' ω 2 = − 1 2 + 40 10 2 2 = 3 cm.
+ Thời điểm lò xo dài nhất lần đầu tiên ứng với thời điểm lần đầu vật đến vị trí biên → Δ t = 180 0 − a r c o s 1 3 360 0 T = 0 , 135
→ Khoảng cách giữa hai vật:
Δ S = v 0 Δ t + 0 , 5 a Δ t 2 – 4 = 3 , 2 c m
Giải thích: Đáp án A
Phương pháp : Áp dụng định luật II Niuton, lí thuyết về chuyển động th ẳng nhanh dần đều , hê ̣thức độc lập theo thời gian của x vàv để tính biên độ. Áp dụng công thức tính vận tốc cực đại của con lắc lò xo dao động điều hoà.
Cách giải:
Viết phương trình 2 Niuton cho vật nặng ta được: P – N – Fđh = ma
Khi vật bắt đầu rời tấm ván thì N = 0. Khi đó : P – Fdh ma mg k l ma l 0, 08m 8cm
Với chuyển động nhanh dần đều có vận tốc đầu bằng 0 ta áp dụng công thức:
Ta có ω = 10 rad/s , vị trí cân bằng của vật lò xo dãn: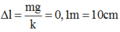
Tại thời điểm vật rời ván ta có: x = -0,02m;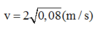
Biên độ dao động: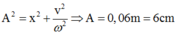
Vận tốc cực đại của vât: