K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

VT
6 tháng 8 2017
Đáp án A
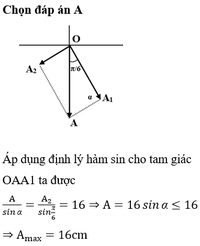
Giản đồ vecto:
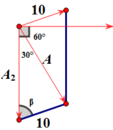
Áp dụng ĐL hàm sin:
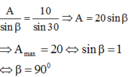
Theo đề bài, A chỉ bằng 1 nửa giá trị max A = 10 c m


VT
29 tháng 7 2018
Đáp án D
Biên độ dao động tổng hợp được tính theo công thức sau:
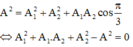
Để PT ẩn A 1 có nghiệm:
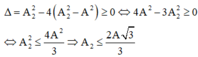
Do đó 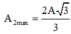
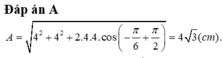
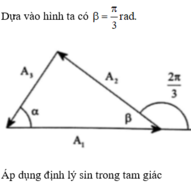
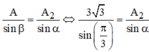
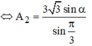
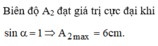

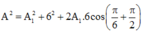
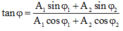
+ Từ hình vẽ, áp dụng định lý hàm cos trong tam giác ta có:
A12 = A22 + A2 - 2A2Acos(A,A2)
+ Phương trình trên luôn có nghiệm nên:
D = 3A2 - 4(A2 - 100) ³ 0 ® A £ 20 ® Amax = 20 cm