Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Delta\varphi=\varphi_2-\varphi_1=\dfrac{\pi}{2}\)
\(A=\sqrt{A_1^2+A_2^2}=6\sqrt{2}\left(cm\right)\)
Phương trình dao động tổng hợp: \(x=6\sqrt{2}cos\left(5\pi t+\dfrac{\pi}{2}\right)cm\)
Cơ năng dao động của vật là:
\(W=\dfrac{1}{2}m\omega^2A^2=\dfrac{1}{2}.0,2.\left(5\sqrt{10}\right)^2.\left(6\sqrt{2}.10^{-2}\right)^2=0,18\left(J\right)=180\left(mJ\right)\)
Chọn A.

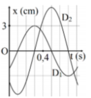
- Ta có: 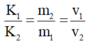
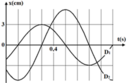
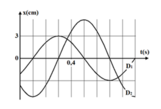
- Từ đồ thị ta thấy: A1 = 3 cm.
- Cũng theo đồ thị thì ta thấy cứ một ô ngang theo trục thời gian là 0,1s.
- Quan sát đồ thị ta thấy thời gian dao động D2 đi từ VTCB ra biên mất thời gian là 2 ô nên:
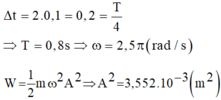
- Gọi Δ1 là thời gian kể từ lúc D1 bắt đầu dao động đến khi lần đầu tiên qua VTCB:
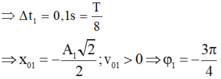
- Gọi Δ2 là thời gian kể từ lúc D2 bắt đầu dao động đến khi lần đầu tiên đến biên âm:
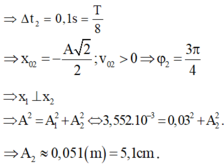

Đáp án A
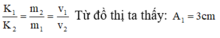
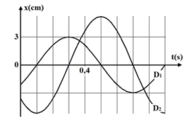
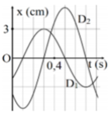
Cũng theo đồ thị thì ta thấy cứ một ô ngang theo trục thời gian là 0,1s
Quan sát đồ thị ta thấy thời gian dao động D 2 đi từ VTCB ra biên mất thời gian là 2 ô nên :
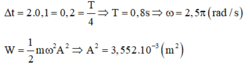
Gọi ∆ t 1 là thời gian kể từ lúc D 1 bắt đầu dao động đến khi lần đầu tiên qua VTCB:
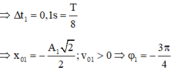
Gọi ∆ t 2 là thời gian kể từ lúc D 2 bắt đầu dao động đến khi lần đầu tiên đến biên âm
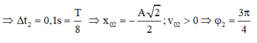


Giải thích: Đáp án A
Phương pháp: Công thức tính cơ năng ![]()
Cách giải:
Theo bài ra ta có: m = 200kg; A1 = 3 cm; T1 = 0,8s ![]()
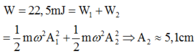

Đáp án A
Theo bài ra ta có
![]()
![]()
![]()
Tại thời điểm t = 0,1s
![]()
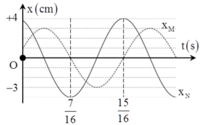
Ta có 2 phương trình dao động:
![]()
Suy ra hai dao động này vuông pha:
![]()
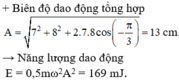


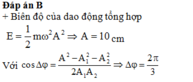

Đáp án C